Определение: Уравнение (2) назвается характеристическим уравнением по отношению к уравнению (1).
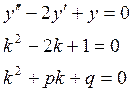
1) ![]()
![]() и
и ![]() -
действительные и различные
-
действительные и различные
2) ![]()
![]() и
и ![]() -
комплексно сопряженные
-
комплексно сопряженные
3) ![]()
![]() и
и ![]() -
действительные равные
-
действительные равные
1) ![]()
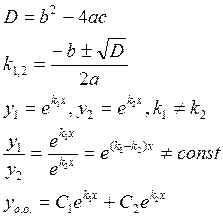
Пример:
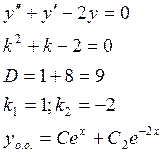
2) ![]()
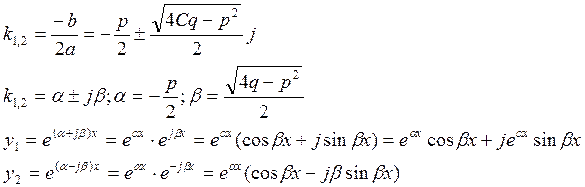
![]() и
и ![]() - комплексные функции действительного
аргумента х.
- комплексные функции действительного
аргумента х.
![]() ,
где
,
где ![]() и
и ![]() -
функции действительного аргумента
-
функции действительного аргумента
Покажем, что если какая-либо
функция действительного аргумента у, удовлетворяет уравнению (1), то функции ![]() и
и ![]() также
будут удовлетворять уравнению (1).
также
будут удовлетворять уравнению (1).
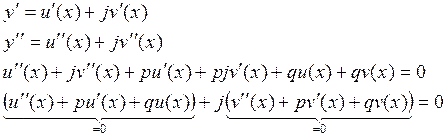
![]()
![]()
Их отношение не равно константе,
следовательно ![]() и
и ![]() линейно
независимы и тогда по теореме 6:
линейно
независимы и тогда по теореме 6:
![]()
Пример:
№1.
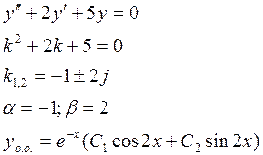
№2.
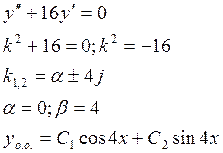
3) ![]()
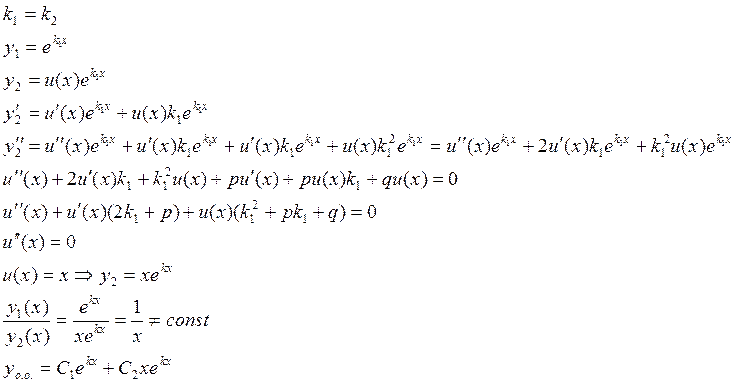
Пример:
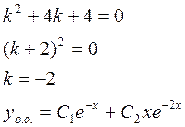
Общее решение ЛОДУ n-ного порядка с постоянными коэффициентами
![]() (1)
(1)
1) составляют характеристическое уравнение
2) находим корни характеристического уравнения а) корни характеристического уравнения (ху) действительные и различные.
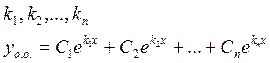
б) Корни х и у действительные и среди них есть кратные.
Каждому корню ![]() соответствует кратность
соответствует кратность ![]() ,тогда частные решения
,тогда частные решения ![]() из которых составляется
из которых составляется ![]() , есть функции
, есть функции ![]()
![]()
корни ху комплексно сопряженные.
в)
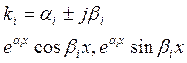
г) корни ху кратные и комплексно
сопряженные . каждому корню ![]() , соответствует
кратность
, соответствует
кратность ![]() , тогда
, тогда ![]()
![]()
Пример:
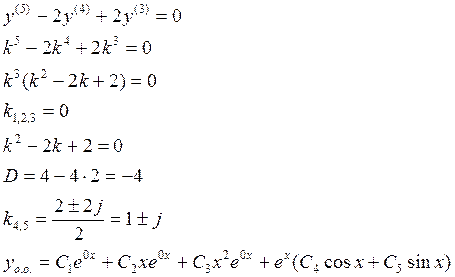
ЛНДУ второго порядка с постоянными коэффициентами
![]() (1)
(1)
Теорема: общее решение ЛНДУ с
постоянными коэффициентами есть сумма общего решения соответствующего
однородного и частного решения неоднородного уравнения ![]() (2)
(2)
Доказательство: Покажем, что функция (2) есть решение уравнения (1)
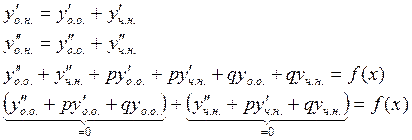
Равенство верно, формула (2) действительно верна.
2) Покажем, что 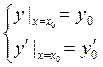
Можно так подобрать значения постоянных, чтобы условия выполнялись
![]()
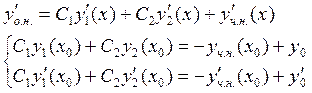
Система имеет единственное
решение, если ![]() .
.
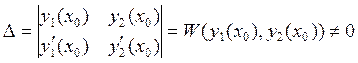
W
составляется из линейно независимых решений ![]() и
и ![]() .
.
По теореме 5 этот определитель не
равен нулю, следовательно каковы бы ни были начальные условия соответствующие
значения постоянных ![]() и
и ![]() всегда
можно найти.
всегда
можно найти.
ЛНДУ второго порядка со специальной правой частью
![]()
I. ![]()
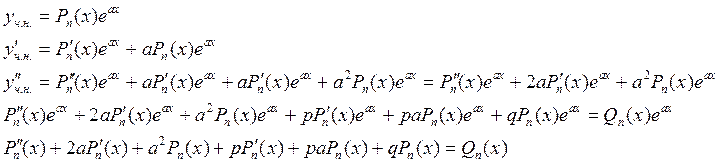
1) а – не корень ху ![]() , следовательно тогда справа многочлен n-ной степени и слева тоже. Степени многочленов совпадают,
следовательно
, следовательно тогда справа многочлен n-ной степени и слева тоже. Степени многочленов совпадают,
следовательно ![]()
2) а – простой корень ху - ![]()
Слева многочлен степени n-1, а справа многочлен степени n,
такого быть не может, следовательно ![]()
3) а – кратный корень ху - ![]() ,
, ![]() следовательно
следовательно
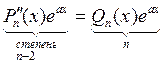 следовательно
следовательно
![]()
Коэффициент многочлена ![]() находится по схеме: ищут
находится по схеме: ищут ![]() и
и ![]() ,
подставлябт производные и
,
подставлябт производные и ![]() в исходное уравнение
и приравнивают коэффициенты при одинаковых степенях х.
в исходное уравнение
и приравнивают коэффициенты при одинаковых степенях х.
Пример:
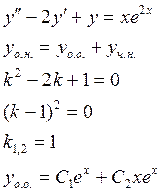
2 – не корень ху, следовательно домножать на х не надо
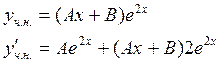
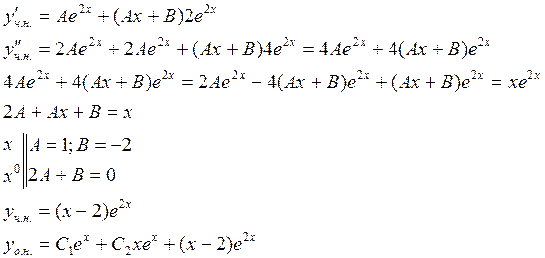
Пример 2:
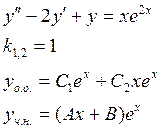
1 – кратный корень ху,
следовательно ![]()
…………………………………………………
Пример 3:
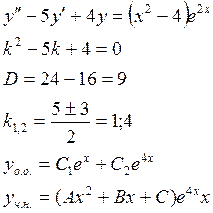
т.к. 4 – совпадает с одним из корней, следовательно домножаем на х.
Пример 4:
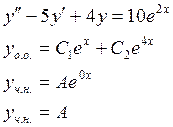
…………………………………
II. ![]()
1) ![]() - не
корень
- не
корень
![]()
![]() и
и ![]() - многочлены степени р с
неизвестными коэффициентами
- многочлены степени р с
неизвестными коэффициентами
2) ![]()
![]()
Пример:
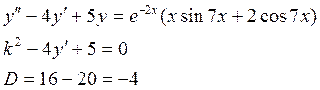
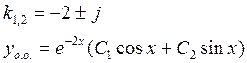
![]() - не
корень
- не
корень
![]()
Теорема: Пусть правая часть ![]() представлена в виде суммы двух функций
представлена в виде суммы двух функций ![]() , тогда
, тогда ![]() есть
сумма
есть
сумма ![]() -ных следующих уравнений
-ных следующих уравнений
![]()
Пример:
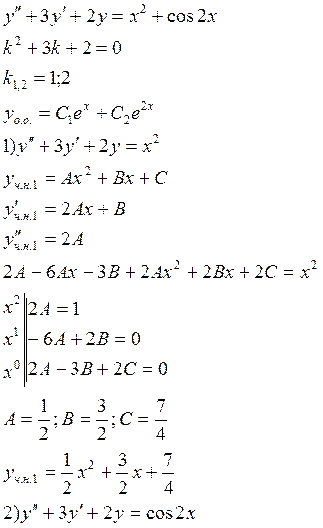
![]() - не
корень ху.
- не
корень ху.
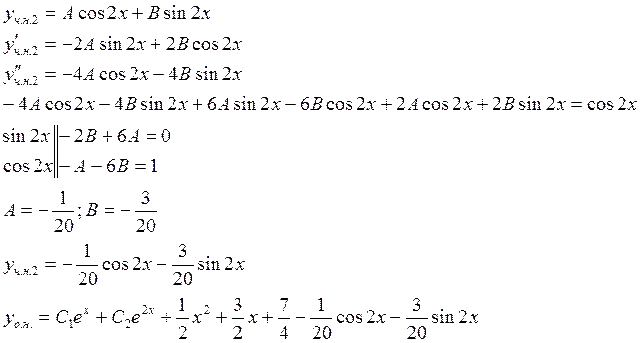
Для нахождения решений задачи Коши необходимо:
1) составить ху и найти его корни
2) по корням составить ![]()
3) по виду правой части выписать ![]()
4) выписать ![]() как сумму
как сумму ![]()
5) подставить заданное начальное
условие найти значение коэффициентов ![]() и
и ![]()
Гармонические колебания
Свободные гармонические колебания
описываются уравнением ![]() , а вынужденные гармонические
колебания уравнением
, а вынужденные гармонические
колебания уравнением ![]() ,
, ![]() -
частота собственных колебаний системы,
-
частота собственных колебаний системы, ![]() -
частота вынужденных колебаний.
-
частота вынужденных колебаний.
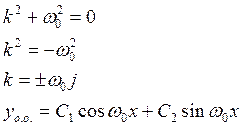
А) пусть ![]() следовательно
следовательно
![]() - не корень ху.
- не корень ху.
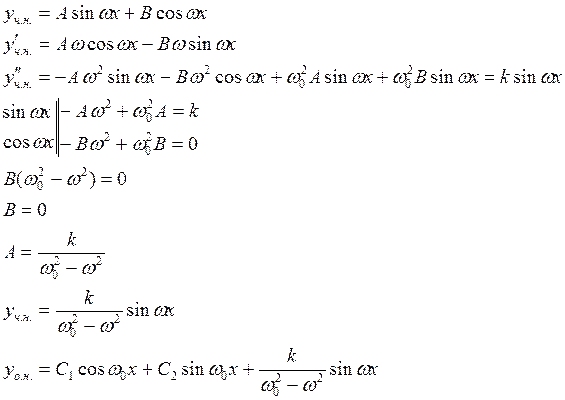
Решение ограничено при ![]() .
.
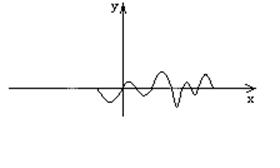
Б) Пусть ![]() -
корень ху.
-
корень ху.
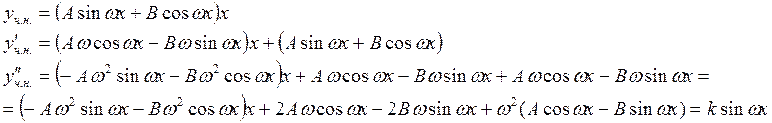
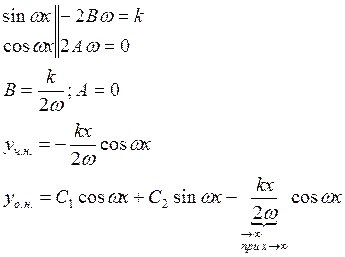
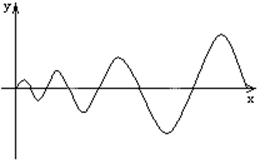
Решение неограниченно возрастает
при ![]() .
.
Метод вариации произвольных постоянных
![]()
![]()
чтобы подобрать ![]() считаем
считаем ![]() и
и ![]() не постоянными, а функциями
не постоянными, а функциями ![]()
![]()
Пусть ![]()
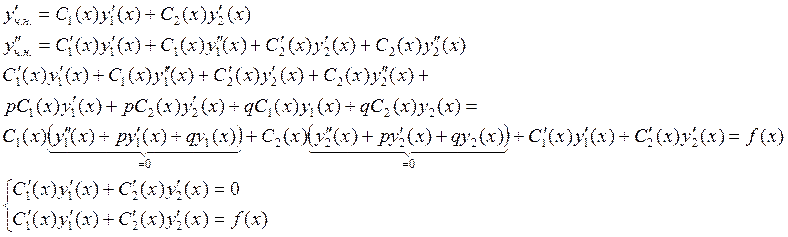 Система
имеет единственное решение т.к. ее определителем является определитель W, а он отличен от нуля на решенных
Система
имеет единственное решение т.к. ее определителем является определитель W, а он отличен от нуля на решенных ![]() и
и
![]() однородного уравнения.
однородного уравнения.
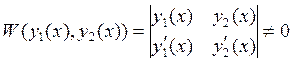
Функции ![]() и
и
![]() получаются интегрированием решений
системы и при интеграле постоянные не пишутся.
получаются интегрированием решений
системы и при интеграле постоянные не пишутся.
Пример:
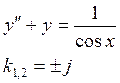
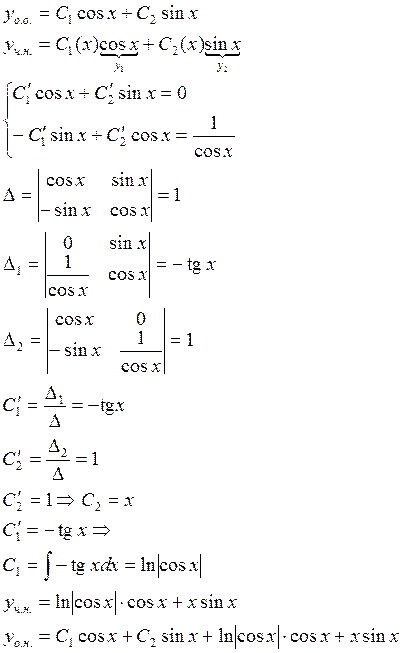
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.