Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных, страница 11

.

Бесконечный ряд стоящий в правой части называется рядом Тейлора функции . Если , то получаем частный случай ряда Тейлора:  - называемый рядок Маклорена.

Примеры разложения функций в степенной ряд

1)   

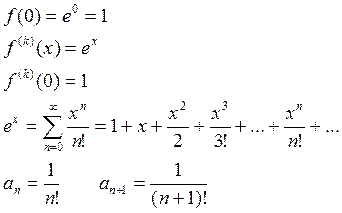
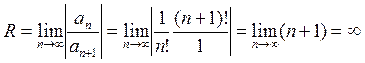 - ряд для  абсолютно сходящийся при всех х.

Пример:

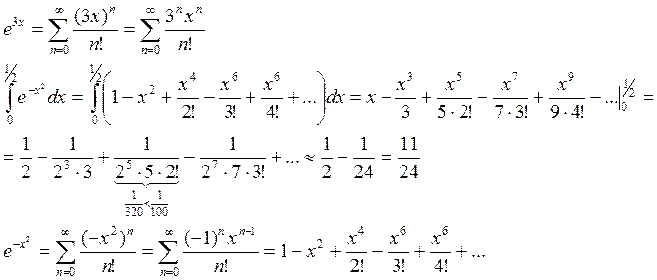
2)    

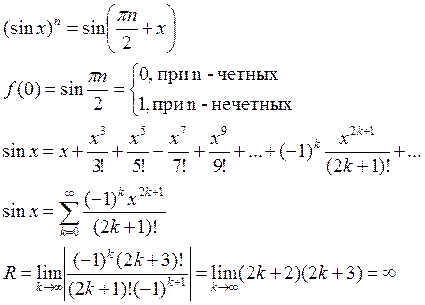
ряд абсолютно сходится при любых х.

3)      

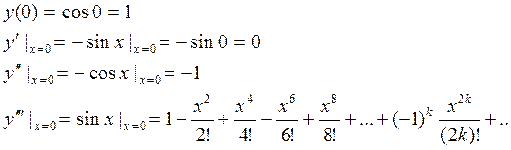
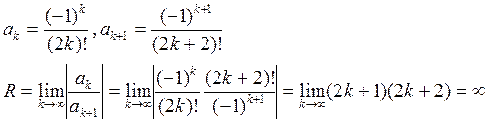
Ряд абсолютно сходится для любых х.

4)

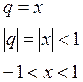
5)

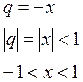
6)        

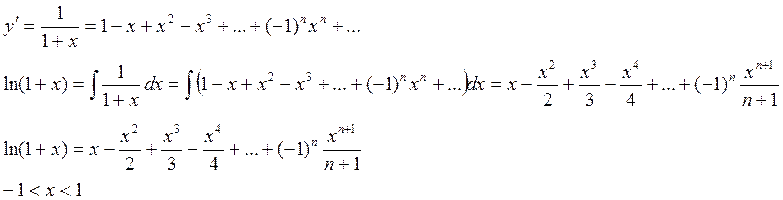Пример:

 - погрешность порядка тысячных

7)   

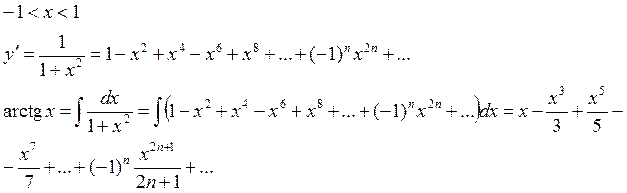
Пример:

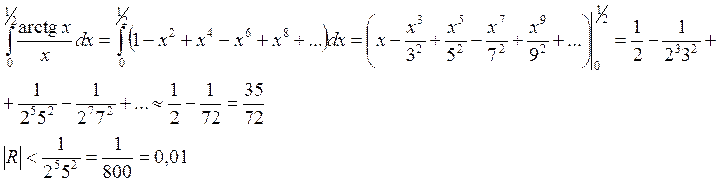
8)    

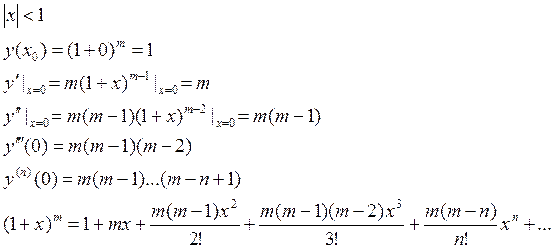
Пример:

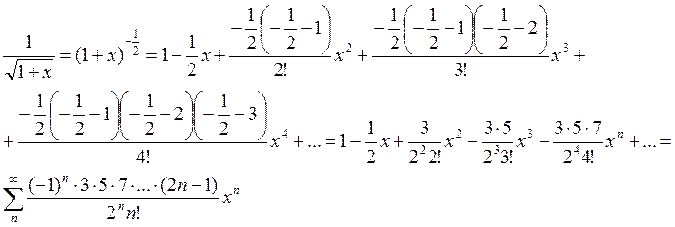
Применение степенных рядов

Ряды применяются для:

1) приближенных вычислений значения функции (см. пример )

2) приближенного вычисления интегралов (см. )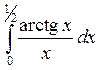

3) приближенного решения алгебраических и дифференциальных уравнений при этом искомую функцию и все ее производные представляют в виде степенного ряда с неизвестными коэффициентами, остальные функции входящие в уравнение также раскладываются в степенной ряд и приравнивают коэффициенты при одинаковых степенях х.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ДУ)

Определение: Дифференциальным уравнением называется уравнение связывающее независимую переменную х, неизвестную функцию  и ее производные .

Символически дифференциальное уравнение записывается в виде - ДУ n-ного порядка

Определение: Порядком ДУ называется порядок наивысшей производной входящей в него.

Решением или интегралов ДУ называется всякая функция вида , которая будучи подставленной в уравнение обращает его в тождество.

ДУ первого порядка

ДУ первого порядка называется уравнение вида .

Если из этого уравнения можно выразить  , т.е. , то ДУ газывается разрешенным относительно производной.

Теорема: Если в уравнении (1) функция  и ее частная производная  непрерывна в некоторой области D на плоскости хОу содержащей некоторую точку , то существует единственное решение этого уравнеия  удовлетворяющая условию, что при ,  у должен быть равен .

Геометрический смысл теоремы: Существует и при том единственный у удовлетворяющий уравнению (1), график которой проходит через точку с координатами .

Определение: Условие, что при , функция у должка быть равна некоторому заданному числу  называемым начальным условием и записывают .

Задачей Коши называют следующую задачу:

Найти решение  ДУ (1) удовлетворяющее начальному условию .

Общим решением ДУ первого порядка называют функцию  зависящее от одного произвольного постоянного с и удовлетворяющим условию:

1) она удовлетворяет ДУ при любом конкретном значении с.

2) каково бы ни было начальное условие можно найти такое значение , что функция  удовлетворяет задаче Коши.

Равенство вида , не явно задающее общее решение ДУ, называемым общим интегралом ДУ.

Определение: Частным решением ДУ называется функция , которое получается, если в общем решении произвольной постоянной придать конкретное значение .

Соотношение вида  называется частным интегралом ДУ.

Решить задачу Каши, означает найти частное решение ДУ  для каждой точки .

Уравнение (1) определяет значение производной , т.е. угловой коэффициент косательной.

Т.е. уравнение (1) дает совокупность направлений или поле направлений на плоскости хОу, следовательно решить ДУ означает найти семейство кривых направляющих касательные к которым, совпадает с направлением поля в соответствующих точках.

Общий интеграл – семейство кривых зависящих от одной произвольной константы С.

Эти кривые называются интегральными кривыми данного ДУ.

Частный интеграл – одна кривая проходящая через заданную точку

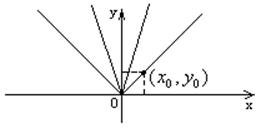
Уравнения с разделяющимися переменными

Вид:     (2)

Определение: ДУ вида (2) называют уравнением с разделяющимися переменными.

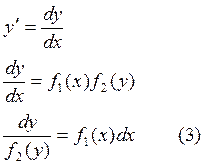
Равенство (3) рассматривается как равенство дифференциалов, следовательно неопределенный интеграл от обеих частей равенства (3) будут отличны лишь константой.

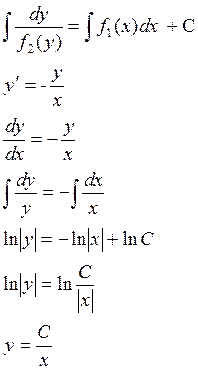
К уравнениям с разделяющийся переменной также относятся уравнения вида

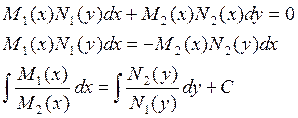
Пример:

найти общее решение ДУ.

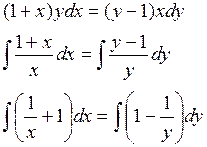
 - общий интеграл ДУ.

Однородные ДУ первого порядка

Определение: уравнение вида  называется однородным относительно х и у, если правая часть при любых  удовлетворяет тождеству .