Принцип решения:
![]() ,
тогда подставим
,
тогда подставим ![]()
Замена: ![]() или
или
![]()
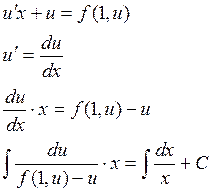
![]() замена,
сводящая однородное уравнение к линейному..
замена,
сводящая однородное уравнение к линейному..
Пример: ![]()
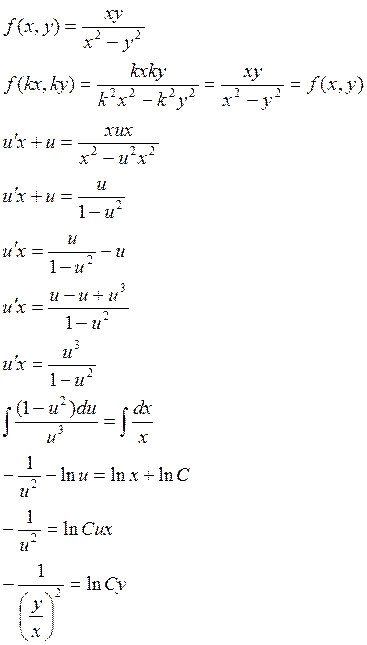
Линейное ДУ первого порядка
Определение: Линейным называется
уравнение линейное относительно неизвестной функции и ее производной, т.е.
уравнение вида ![]() , где
, где ![]() и
и
![]() заданные непрерывные функции.
заданные непрерывные функции.
Решение линейного уравнения ищут в виде
![]()
![]()
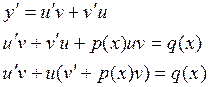
будем выбирать ![]() так, чтобы
так, чтобы ![]()
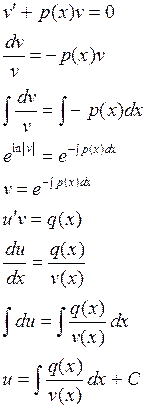
Пример:
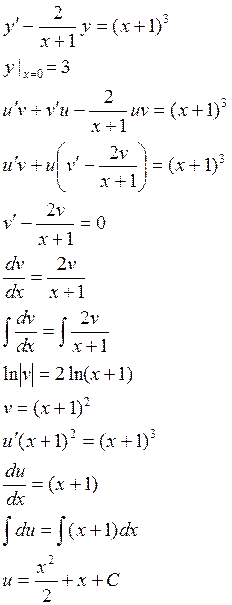
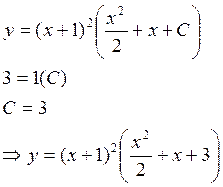
Уравнение Бернулли
Уравнение вида ![]() , называют уравнением Бернулли,
, называют уравнением Бернулли, ![]() и
и ![]() заданные
непрерывные функции.
заданные
непрерывные функции.
![]()
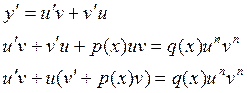
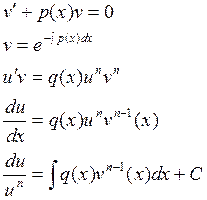
Пример: решить уравнение
![]()
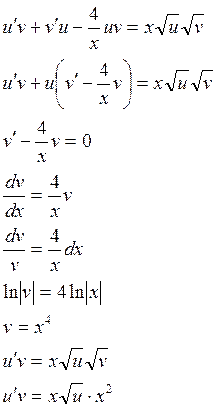
![]()
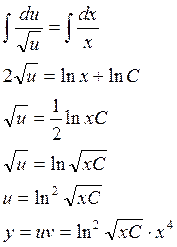
ДУ высших порядков
ДУ n-ного
порядка символически записываетсяв виде ![]() или
если оно разрешено относительно n-ной производной, то
или
если оно разрешено относительно n-ной производной, то ![]() (1).
(1).
Теорема: Если функция ![]() и ее частные производные по аргументам
и ее частные производные по аргументам ![]() непрерывны в некоторой области
содержащей значение
непрерывны в некоторой области
содержащей значение
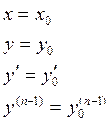
то существует единственное
решение ![]() уравнения (1), удовлетворяющее условию
уравнения (1), удовлетворяющее условию
![]()
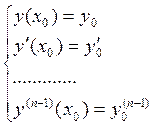
Эти условия называются начальными условиями.
![]() - ДУ
второго порядка.
- ДУ
второго порядка.
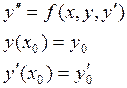
![]() -
заданные числа
-
заданные числа
Определение: общим решением уравнения n-ного порядка, называется функция, зависящая от n произвольных постоянных, если
1) она удовлетворяет уравнению при любых значениях постоянных
2) при заданных начальных условиях
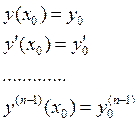
постоянные ![]() , можно подобрать так чтобы функция
, можно подобрать так чтобы функция ![]() , удовлетворяла этим начальным условиям.
, удовлетворяла этим начальным условиям.
Определение: соотношение вида ![]() неявно определенное общее решение
называется общим интегралом ДУ.
неявно определенное общее решение
называется общим интегралом ДУ.
Всякое решение получающееся из общего при конкретных значениях постоянной, называется частным решением.
Уравнения допускающие понижение порядка
I. ![]() - уравнения не содержащие явным образом
у.
- уравнения не содержащие явным образом
у.
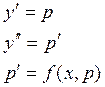
Пусть найдено общее решение этого уравнения:
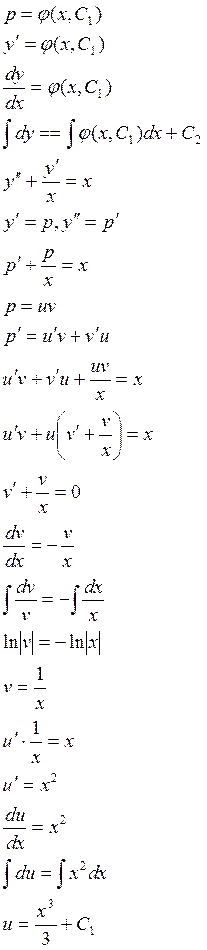
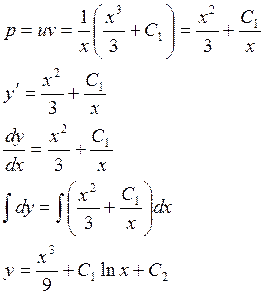
II.
Уравнение вида ![]() - называется уравнениями не
содержащими явным образом независимой переменной х.
- называется уравнениями не
содержащими явным образом независимой переменной х.
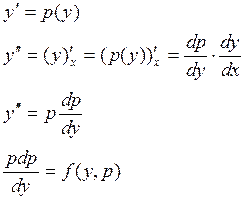
Получим ДУ первого порядка относительно р.
Пусть ![]()
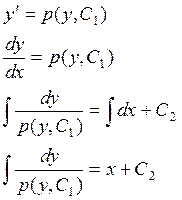
Пример:
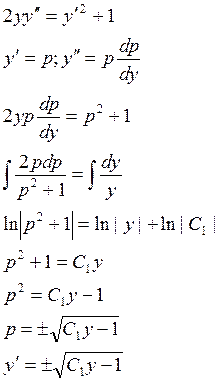
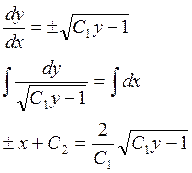
ЛОДУ
Определение: ДУ n-ного
порядка называется линейным, если оно является уравнением первой степени
относительно искомой функции у и ее производноой ![]() ,
т.е. имеет вид
,
т.е. имеет вид
![]() (1)
(1)
Функция ![]() называется
правой частью уравнения (1).
называется
правой частью уравнения (1).
Если ![]() , то
уравнение (1) называется ЛДУ с постоянными коэффициентами.
, то
уравнение (1) называется ЛДУ с постоянными коэффициентами.
![]()
Если ![]() , то
уравнение (1) называется ЛОДУ.
, то
уравнение (1) называется ЛОДУ.
Теорема 1: Если ![]() и
и ![]() -
два частных решения ЛОДУ, то
-
два частных решения ЛОДУ, то ![]() - есть также решение
этого уравнения.
- есть также решение
этого уравнения.
Доказательство:
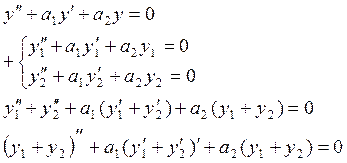
Теорема 2: Если ![]() - решение ЛОДУ и С – некоторая
постоянная, то Су, таже решение ЛОДУ.
- решение ЛОДУ и С – некоторая
постоянная, то Су, таже решение ЛОДУ.
Определение: Два решения ЛОДУ - ![]() и
и ![]() ,
называются линейно независимыми на отрезке
,
называются линейно независимыми на отрезке ![]() , если
их отношение на этом отрезке не является постоянной, т.е.
, если
их отношение на этом отрезке не является постоянной, т.е. ![]() .
.
Определение: Два решения ЛОДУ - ![]() и
и ![]() ,
называются линейно зависимыми на отрезке
,
называются линейно зависимыми на отрезке ![]() , если
, если
![]() .
.
Определитель: 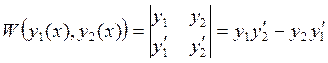 - называется определителем Вронского
или вронскинианом.
- называется определителем Вронского
или вронскинианом.
Теорема 3: Если функции ![]() и
и ![]() ,
линейно независимы на отрезке АВ, то определитель
,
линейно независимы на отрезке АВ, то определитель ![]()
Доказательство:
![]()
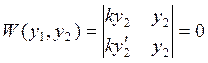
Теорема 4: Если определитель
Вронского ![]() , составленный для решения
, составленный для решения ![]() и
и ![]() ЛОДУ
не равен 0, при каком-либо значении
ЛОДУ
не равен 0, при каком-либо значении ![]() и коэффициенты
уравнения непрерывны, то он не обращается в нуль не при каких значениях
и коэффициенты
уравнения непрерывны, то он не обращается в нуль не при каких значениях ![]() на
на ![]() .
.
Теорема 5: Если решения ![]() и
и ![]() ЛОДУ
линейно независимы на отрезке
ЛОДУ
линейно независимы на отрезке ![]() , то определитель
, то определитель ![]() составленный для этих решений ни
обращается в нуль, не а какой точке
составленный для этих решений ни
обращается в нуль, не а какой точке ![]() .
.
Теорема 6: Если ![]() и
и ![]() , два
линейно независимых решения уравнения
, два
линейно независимых решения уравнения ![]() , то
, то
![]() , где
, где ![]() и
и ![]() - произвольные постоянные, есть его
общее решение.
- произвольные постоянные, есть его
общее решение.
Доказательство: Из теоремы 1 и
теоремы 2 следует, что ![]() есть решение при любых
значениях
есть решение при любых
значениях ![]() и
и ![]() ,
осталось показать, что каковы бы ни были начальные условия
,
осталось показать, что каковы бы ни были начальные условия
![]()
можно так подобрать значения ![]() и
и ![]() ,
чтобы соответствующее частное решение удовлетворяла заданным начальным условиям
,
чтобы соответствующее частное решение удовлетворяла заданным начальным условиям
![]()
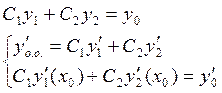
![]() -
решение одно
-
решение одно
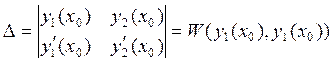
Т.к. функции ![]() и
и ![]() линейно
независимы, то по теореме 5
линейно
независимы, то по теореме 5 ![]() в любой точке,
следовательно система имеет единственное решение
в любой точке,
следовательно система имеет единственное решение ![]() и
и ![]() , чтобы частное решение удовлетворяло
начальным условиям
, чтобы частное решение удовлетворяло
начальным условиям
Пример:
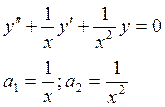
коэффициенты не прерывны на любом
отрезке не содержащем точку 0. (![]() )
)
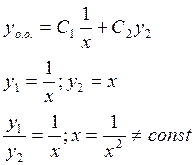
ЛОДУ второго порядка
![]() (1) p и q – константы
(1) p и q – константы
![]()
![]()
![]()
![]() (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.