Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных, страница 10

Функции и  - аналоги коэффициентов Фурье, выражение  - аналог простой гармоники или отдельного члена ряда Фурье.

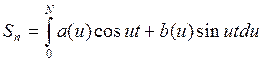
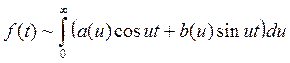 - интеграл Фурье

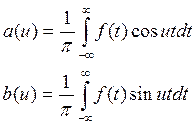
1) Пусть  - четная, тогда

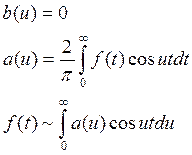
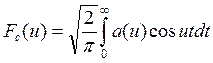 - косинус – преобразование Фурье функции

Функция   называется оригиналом, а  - образом.

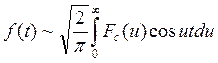
2) Пусть  - нечетная

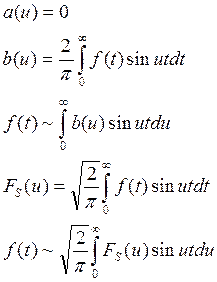
Пример:

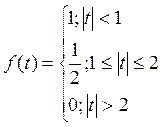
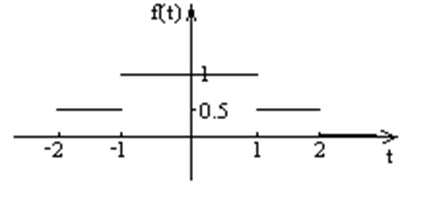
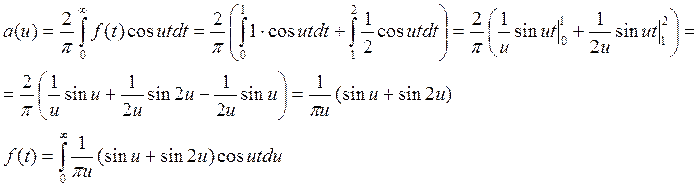
Комплексная форма интеграла Фурье.

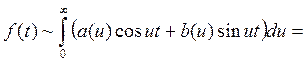
Подствим в этот интеграл формулу Эйлера

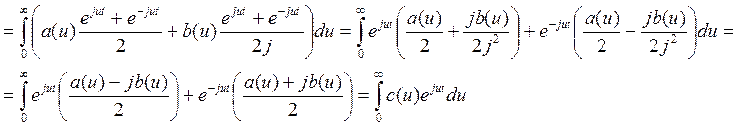
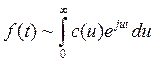
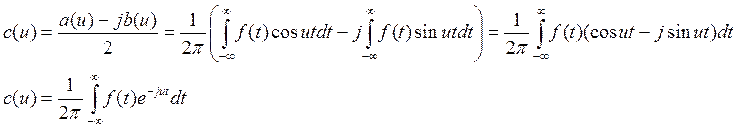
Пример:

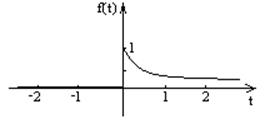
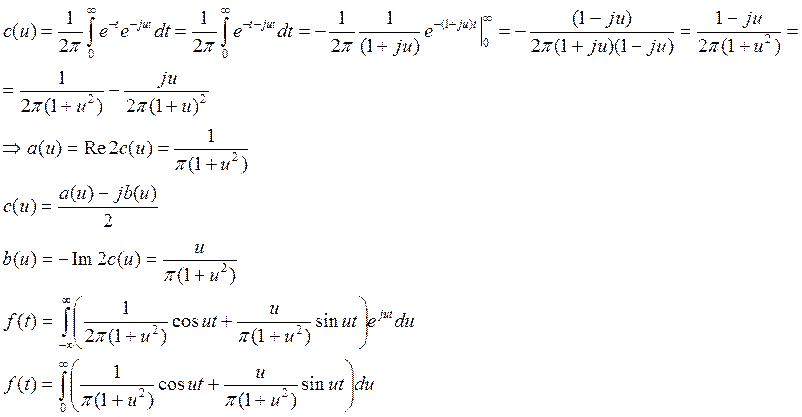
Степенные ряды

Степенным рядом называется функциональный ряд вида

, где  - постоянные числа называемые коэффициентами ряда

Теорема Абеля:

1) если степенной ряд сходится при некотором значении , то он абсолютно сходится, при всяком х, для которого

2) если степенной ряд расходится при некотором значении , то он расходится и при всяком х так что

Доказательство:

1)  - сходится то

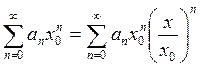
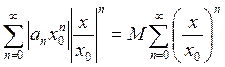
Последний ряд представляет собой геометрическую прогрессию со знаменателем , поэтому последний ряд сходится. Предыдущий ряд сходится по признаку сравнения, исходный ряд абсолютно сходящийся.

2) Предположим в точке  данный степенной ряд расходится

 - расходится.

Предположим противное: при некотором , такой что  ряд сходится, следовательно ряд должен сходится и в точке  ?!

Из теоремы Абеля следует, сто есть такое число R, что при всех , ряд абсолютно сходится и при всех , ряд расходится.

Следствие: областью сходимости степенного ряда является интервал с центом в начале координат, длиной 2R.

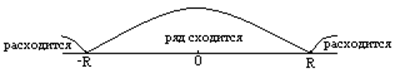
Определение: Интервалом сходимости степенного ряда называется такой интервал , что для всякой точки х, лежащей внутри этого интервала ряд сходится абсолютно, а для всяких х, лежащих вне его расходится.

Число R, называется радиусом сходимости степенного ряда.

Рассмотрим ряд , для него составим ряд из модулей . Применим к последнему ряду признак Деламбера.

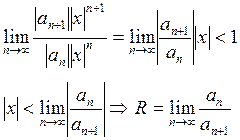
Аналогично применяя радикальный признак Каши получим:

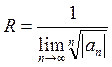
Пример: Найти радиус сходимости и интервал сходимости степенного ряда.

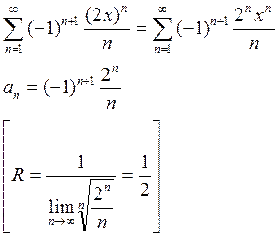
Пусть   

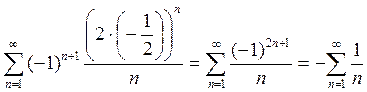
При  ряд расходится.

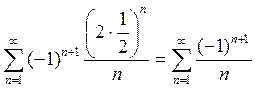  - знакочередующийся ряд. Нет абсолютной сходимости.

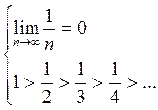
При  ряд сходится условно по признаку Лейбница.

Теорема: Степенной ряд мажорируем на любом отрезке  целиком лежащем внутри интервала сходимости.

Следствие 1: На всяком отрезке целиком лежащем внутри интервала сходимости, сумма степенного ряда есть непрерывная функция.

Следствие 2: Если пределы интеграла  лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов этого ряда.

Следствие 3: Если степенной ряд  имеет интервал сходимости , то ряд , полученный почленным дифференцированием первоначального ряда имеет тот же интервал сходимости , причем  при .

Определение: Степенным рядом по степеням  называют ряд вида

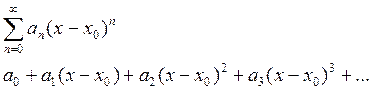
Существует интервал  с центром в точке , такой что в каждой точке этого интервала, ряд сходится абсолютно.

Этот интервал называется интервалом сходимости степенного ряда. Число R-радиус сходимости степенного ряда и в интервале сходимости для ряда по степеням  справедливы все свойства степенных рядов.

Пример: 1) Найти интервал сходимости степенного ряда.

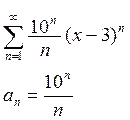
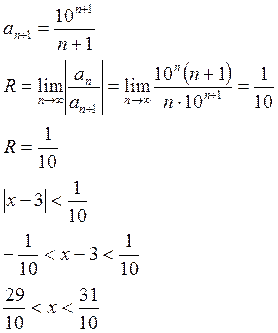
Пусть  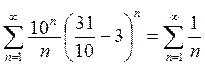       - расходится

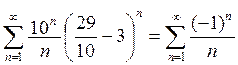      - нет абсолютной сходимости

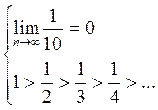
Ряд сходится условно по признаку Лейбница.

2) Найти интервал сходимости степенного ряда.

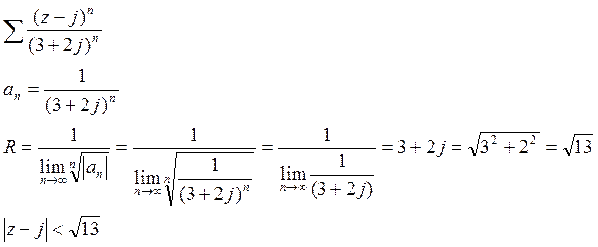
Формула Тейлора и Маклорена

Пусть функция  имеет непрерывную производную всех порядков до  включительно в некоторой окрестности точки .

Представим функцию в виде: , где  - многочлен n-ой степени, причем

,

 - невязка или погрешность приближения.

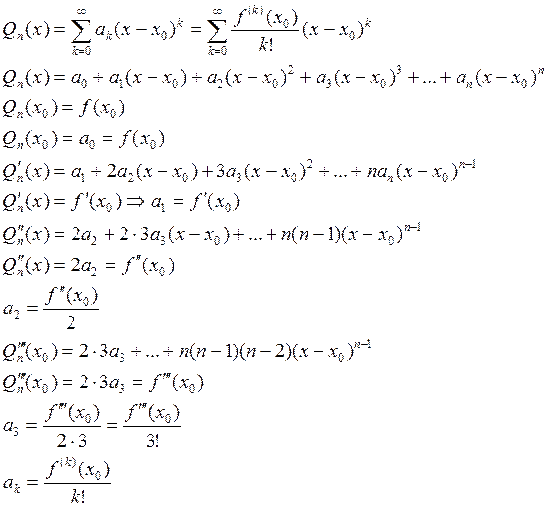
 - многочлен Тейлора в n-ной степени

 - остаточный член формулы Тейлора

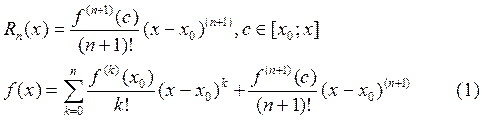
Запись (1) называется формулой Тейлора с остаточным членом Лагранжа.

Теорема: Если функция  - имеет в окрестности точки  непрерывную производную до  включительно, то для любого х из этой окрестности найдется такая точка , что справедлива формула (1).

Пусть функция  имеет непрерывную производную всех порядков в точке , тогда в формуле Тейлора число n может быть сколь угодно большим, и пусть в рассматриваемой окрестности . Перейдем к пределу при  в формуле (1). Получим: