Число ![]() называется корнем многочлена
называется корнем многочлена ![]() , если
, если ![]()
![]()
Теорема 1: При
делении многочлена ![]() на
на ![]() получается
остаток
получается
остаток ![]() , который в точке
, который в точке ![]() равен
равен
![]() .
.
Доказательство:
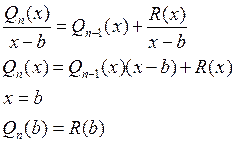
Следствие:
Если число b, является корнем многочлена ![]() , то многочлен
, то многочлен ![]() делится
на
делится
на ![]() без остатка.
без остатка.
b- корень/
![]()
Теорема 2: Всякий многочлен имеет хотя бы один корень – действительный или комплексный.
![]()
Следствие:
Каждый многочлен можно разложить на множители по формуле: ![]() .
.
1) Пусть среди
действительных корней есть кратные, тогда ![]() .
.
![]() кратно
кратно ![]()
![]() кратно
кратно ![]()
……………
![]() кратно
кратно ![]()
2) Пусть у
многочлена пара корней комплексносопряженные, т.е ![]() .
.
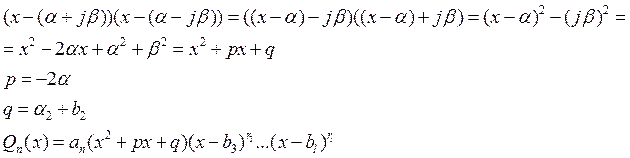
3) Среди
комплексно сопряженных корней есть кратные ![]() .
.
Пример: разложить на множители
![]()
Замечание: Оставляют в разложении только те квадратные трехчлены, у которых нет действительных корней.
Неопределенный интеграл.
![]()
Х – пространство дифференцируемых функций
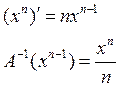
![]()
Определение 1:
Функция ![]() называется первообразной от функции
называется первообразной от функции ![]() на отрезке
на отрезке ![]() , если
во всех точках этого отрезка выполнятся равенство
, если
во всех точках этого отрезка выполнятся равенство ![]() .
.
Пример:
![]() - первообразная для
- первообразная для ![]() .
.
Теорема 1
(Первообразная не единственна): Если ![]() и
и ![]() две первообразные функции
две первообразные функции ![]() на отрезке
на отрезке ![]() , то
разность между ними равна константе.
, то
разность между ними равна константе.
Доказательство:
![]() и
и ![]()
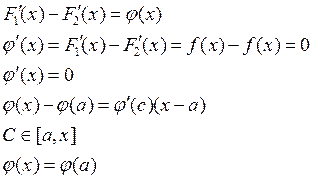
![]() следовательно
следовательно ![]() -
константа.
-
константа.
![]()
Следовательно,
если для функции ![]() известна какая-либо
первообразная, то любая другая первообразная задается формулой
известна какая-либо
первообразная, то любая другая первообразная задается формулой ![]() .
.
Определение:
Если функция ![]() является первообразной для функции
является первообразной для функции ![]() , то она называется неопределенным
интегралом от
, то она называется неопределенным
интегралом от ![]() и обозначается
и обозначается ![]() .
.
![]() , где
, где ![]()
Функция ![]() - называется подынтегральной функцией, а
выражение
- называется подынтегральной функцией, а
выражение ![]() - подынтегральным выражением.
- подынтегральным выражением.
Определение
(2): Неопределенный интеграл есть функция семейства вида ![]() , где
, где ![]() или
совокупность первообразных.
или
совокупность первообразных.
Первообразная
существует не для всякой функции, но если функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() , то для этой функции первообразная
существует.
, то для этой функции первообразная
существует.
Нахождение
первообразной для функции ![]() , называется интегрированием
функции
, называется интегрированием
функции ![]() . Если производная от элементарной
функции всегда есть элементарная функция, то первообразная от элементарной
функции может оказаться не элементарной функцией.
. Если производная от элементарной
функции всегда есть элементарная функция, то первообразная от элементарной
функции может оказаться не элементарной функцией.
Из определения (2) следуют свойства:
1) Производная от неопределенного интеграла равна подынтегральной функции.
![]()
2) Дифференциал от неопределенного интеграла равен подынтегральному выражению.
![]()
3) Неопределенный интеграл от дифференциала некоторой функции равен самой этой функции плюс произвольная постоянная.
![]()
Таблица интегралов.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
Доказательство:
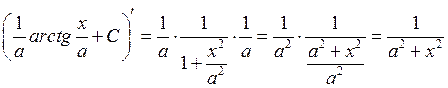
11) ![]()
12) ![]()
13) ![]()
14) ![]()
Некоторые свойства неопределенного интеграла.
Теорема 1: Неопределенный интеграл от суммы двух или нескольких функций равен сумме их интегралов.
![]()
Доказательство:
![]()
![]()
Теорема 2:Постоянный множитель можно выносить за знак неопределенного интеграла.
![]()
Доказательство:
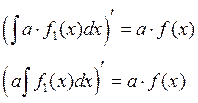
Теорема 3:
Если ![]() , то
, то ![]() .
.
Доказательство:
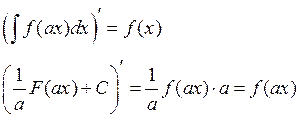
Пример: ![]()
Теорема 4: Если
![]() , то
, то ![]() .
.
Доказательство:
![]()
![]()
Пример: ![]()
Теорема 5:
Если ![]() , то
, то ![]() .
.
Пример: ![]()
Теорема 6:
Любая формула таблицы интегралов сохраняет свой вид, если вместо переменной в
левую и правую части поставить ![]() , где
, где ![]() - дифференцируемая функция.
- дифференцируемая функция.
Пример:
1) ![]()
2) ![]()
3) ![]()
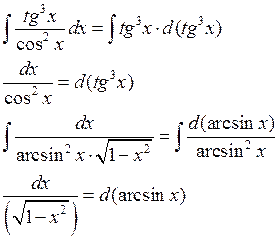
Интегрирование методом замены переменных или методом подстановки.
Теорема: Пусть![]() где
где ![]() -
непрерывная функция с непрерывной производной имеющей обратную функцию, тогда
-
непрерывная функция с непрерывной производной имеющей обратную функцию, тогда ![]() .
.
Доказательство:
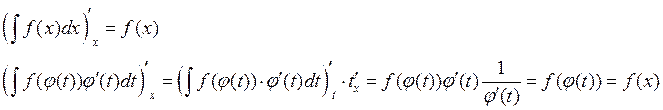
Пример:
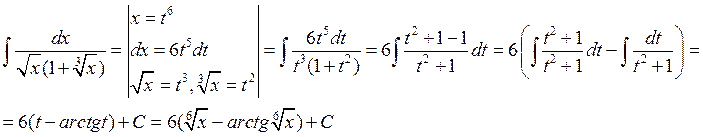
Замечание:
![]()
Пример:
![]()
![]()
Интегрирование по частям.
Пусть
подынтегральная функция ![]() представима в виде
представима в виде ![]() , где
, где ![]() и
и ![]() - дифференцируемые функции, тогда
- дифференцируемые функции, тогда ![]()
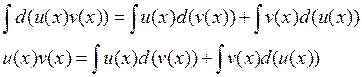
![]() -
формула интегрирования по частям.
-
формула интегрирования по частям.
Пример:
1) 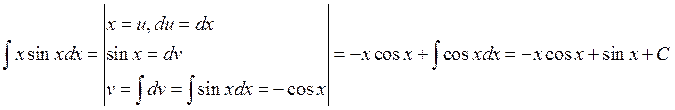
2) 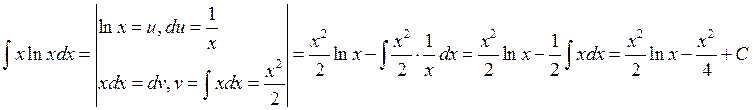
3) 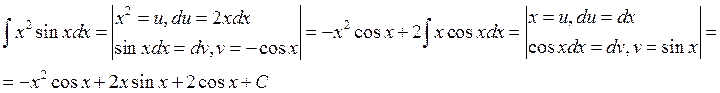
Если после первого применения формулы интегрирования по частям функция упростилась, но еще не получается табличного интеграла, то формулу применяют еще раз.
I. 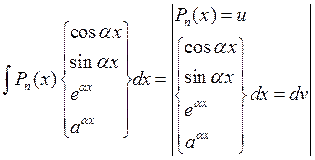
II. 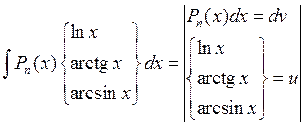
III.![]()
Пример:
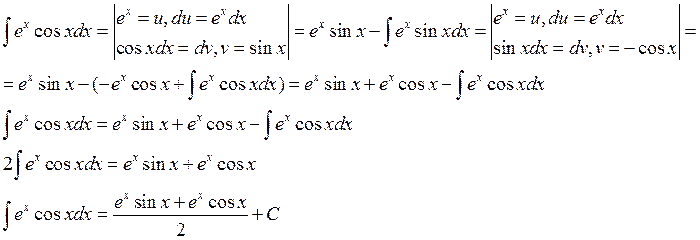
Интегралы от некоторых функций содержащих квадратный трехчлен.
I. 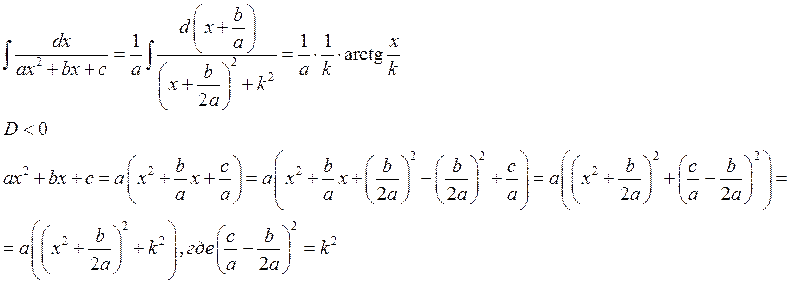
Пример:
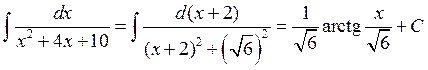
II
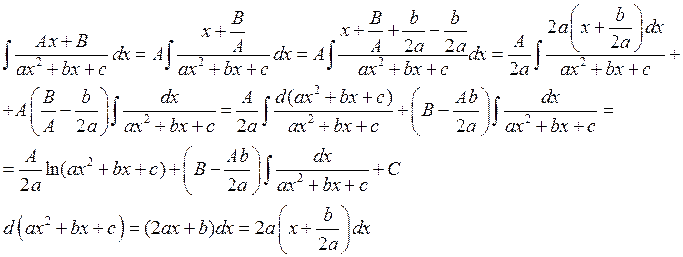
Пример:
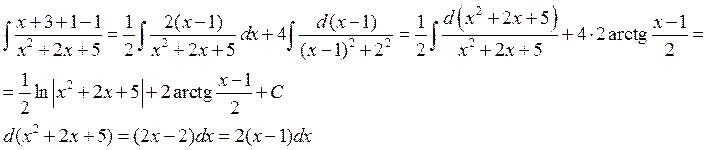
III. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.