Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных, страница 8

Доказательство:

Рассмотрим

Из условия (2) следует, что каждая скобка положительна и последовательность  возрастает с возрастанием m.

В силу условия (2) каждая скобка положительна, поэтому  не превосходит .

Последовательность частичных сумм  возрастает и ограничена сверху числом , поэтому

Рассмотрим последовательность нечетных частичных сумм .

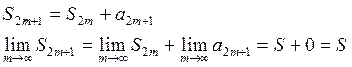
Следовательно, последовательность нечетных сумм тоже сходится к S и S является суммой ряда.

Замечание: Если знакочередующийся ряд удовлетворяет условию теоремы Лейбница, то погрешность замены его суммы S, частичной суммы , оценивается так, т.к. отбросили при построении  все члены ряда начиная с , то отброшенные члены ряда сами образуют бесконечный ряд, сумма которого по абсолютной величине меньше его первого члена, т.е. , следовательно погрешность по абсолютной величине также меньше первого отброшенного члена.

Пример:

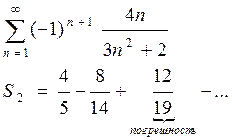
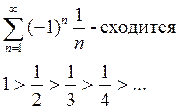
Теорема: Если знакопеременный ряд (1) (- любого знака) таков, что ряд составленный из абсолютных величин его членов (2) сходится, то и данный знакопеременный ряд сходится.

Доказательство:  - частичная сумма (1)

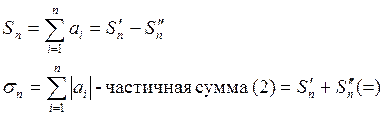
- сумма всех «+»

 - сумма абсолютных величин всех отрицательных членов среди первых n членов.

По условию  имеет предел:

Т.к.  и  - монотонно возрастающие положительные величины и из (=) следует, что они меньше и  имеет предел, то и существует два других предела, значит существует предел их разности и следовательно существует предел .

Пример:

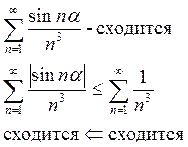
Определение: Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд составленный из абсолютных величин его членов.

Если же знакопеременный ряд сходится, а ряд составленный из абсолютных величин его членов расходится, то данный знакопеременный ряд называется условносходящимся.

 - сходится по теореме Лейбница (условносходящийся интеграл).

 - расходится

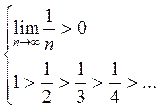
Чтобы исследовать знакопеременный ряд на сходимость, надо:

1) составить ряд из модулей и исследовать на абсолютную сходимость

2) если абсолютной сходимости нет, то исследовать на условную сходимость по признаку Лейбница.

Функциональные ряды

Определение: Ряд вида  называется функциональным рядом.

Совокупность всех значений х, при которых данный ряд сходится называется областью сходимости функционального ряда. В области сходимости сумма ряда есть функция от х.

 - геометрическая прогрессия

 - сходится

 - функциональный ряд. Область сходимости

Определение: Функциональный ряд  называется мажорируемым в некоторой области изменения х, если существует такой сходящийся числовой ряд с положительными членами, что для всех х из данной области и для всех n выполнено неравенство .

Пример:

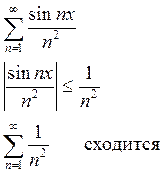
Из определения следует, что ряд мажорируемый в некоторой области абсолютно сходится во всех точках области.

Теорема 1: Сумма ряда непрерывных функций мажорируемых на некотором отрезке [a,b] есть функция непрерывная на этом отрезке.

Теорема 2: Пусть дан ряд непрерывных функций мажорируемый на некотром отрезке [a,b] и пусть S(x) сумма этого ряда, тогда интеграл , по любому отрезку равен сумме таких же интегралов от членов ряда .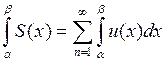

Теорма 3: Если ряд  составлен из функций имеющиз непрерывные производные из отрезков [a,b] сходится на этом отрезке к сумме S(x) и ряд  составленный из производных его членов мажорируем на том же отрезке, то сумма ряда производных от суммы исходного ряда.