Основные законы движения жидкости и газа

                Г л а в а   I

ОСНОВНЫЕ ЗАКОНЫ ДВИЖЕНИЯ ЖИДКОСТИ

И ГАЗА

1.1.  ЗАКОНЫ ПЕРЕНОСА ИМПУЛЬСА,

        ТЕПЛОТЫ И ВЕЩЕСТВА

        режде чем  приступить к рассмотрению  явлений и законов

        газогидромеханики,  напомним  кратко  основные термины

и определения, которыми оперирует эта часть физики.

В механике жидкостей и газов в большинстве случаев жидкость и газ рассматривают как сплошные среды (континуумы), непрерывно распределенные в занимаемом ими объеме, забывая о том, что на самом деле эти вещества состоят из отдельных молекул. Различие между жидкостями и газами с точки зрения механики сводится в основном к различию в их сжимаемости. Под этим термином понимают способность тела изменять объем при постоянной массе. Жидкости подвержены сжатию в небольшой степени, газы – наоборот, изменяют свой объем сравнительно легко. Сжимаемость можно характеризовать коэффициентом объемного сжатия (расширения) , представляющим собой относительное изменение объема при изменении давления (z = p), температуры (z = T) или при совместном их действии. Так, в соответствии с уравнением состояния идеального газа для изотермического сжатия (Т = const) , для изобарического сжатия (р = const) b_р = 1/Т.

Опытным путем было замечено, что если попытаться произвести сжатие газа малым, но резким повышением давления, то возмущение давления распространяется в виде волны. Скорость распространения такого слабого возмущения – скорость звука  – является вполне определенной величиной, зависящей лишь от температуры газа; она тесно связана со сжимаемостью и характеризует упругие свойства среды:

.

Здесь  k – отношение  теплоемкостей;   k = c_p /c_V; R₀ – удельная газовая постоянная; r – плотность среды. Для воздуха k = 1,41, R₀ = 287 Дж/кг×К)  и  = 20,15 .

С коэффициентом объемного расширения b_Т скорость звука связана соотношением

.                  (1.1)

Отсюда видно, что скорость звука меньше у более сжимаемых сред.

Если рассматривается несжимаемая среда (r = const, b_T = 0), к которой с некоторым приближением можно отнести капельные жидкости, то в этом случае употребляют термины гидродинамика или гидромеханика. При описании течения газов с небольшим уровнем скоростей (меньше 150 м/с) зачастую можно пренебречь сжимаемостью газа и считать плотность r постоянной. Поэтому аэродинамика малых скоростей описывается уравнениями гидродинамики. Прикладную гидродинамику называют гидравликой.

При решении задач, где эффектами сжимаемости нельзя пренебречь (околозвуковые и сверхзвуковые скорости), используют уравнения газодинамики. Большие сверхзвуковые и гиперзвуковые скорости (М = U/ > 10) привели к созданию новой дисциплины – аэротермодинамики.

Изучая законы переноса в потоках жидкостей и газов, рассматривают три величины: векторная – импульс, или количество движения,  и две скалярные – теплота и вещество. В движущемся потоке в общем случае наблюдается неоднородность таких величин, как скорость, температура и концентрация вещества. Вследствие этой неоднородности в среде возникают явления переноса импульса, теплоты и вещества. Как и всякие другие теории, теория конвективного теплообмена базируется на ряде гипотез. Эти гипотезы были высказаны Ньютоном, Фурье и Фиком на основании обобщения опытных фактов. Затем они были подтверждены выводами молекулярно-кинетической теории и получили в молекулярной физике название законов переноса.

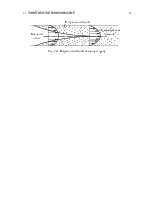
Для простоты будем рассматривать двумерное течение несжима-емой жидкости вдоль пластины (рис. 1.1). Представим, что на пластине имеются участки: адиабатический I, нагреваемый II и учас-ток, где наблюдается диффузия материала стенки (например, сублимация нафталинового покрытия) III.

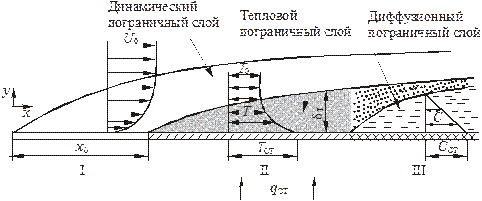
Рис. 1.1. Пограничный слой на пластине: адиабатический участок (I),

нагретый участок (II), участок сублимации (III)

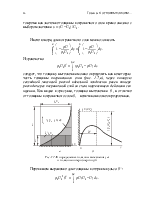
I.  В соответствии с законом Ньютона напряжение трения между двумя соседними слоями жидкости пропорционально градиенту скорости, т.е., грубо говоря, зависят от разности скоростей этих слоев:

.                                             (1.2)

Коэффициент пропорциональности  m  в этом выражении называется динамической вязкостью или коэффициентом внутреннего трения газа. Иногда удобно пользоваться кинематической вязкостью n = m/r.

Жидкости, для которых закон Ньютона не выполняется, называются неньютоновскими, а их течения – реологическими.

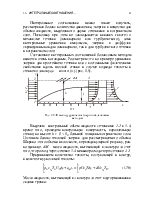
II. Закон теплопроводности Фурье  гласит, что плотность теплового потока, передаваемого путем теплопроводности, т.е. в результате взаимодействия молекул, пропорциональна градиенту температуры:

.                                            (1.3)

Знак «минус» указывает на то, что энергия переносится в направлении снижения температуры. Коэффициент пропорциональности l в этом соотношении называется теплопроводностью.