Другие предметы \ Тепломассообмен

Основные законы движения жидкости и газа, страница 7

На входе в трубу (рис. 1.4) на ее стенке образуется пограничный слой, нарастающий вниз по потоку. Радиус трубы есть верхний предел толщины пограничного слоя. Внутри трубы, вне пограничного слоя, существует внешний поток, который исчезнет, когда пограничные слои сомкнутся. Вниз по потоку за этим сечением не будет внешнего потока, там будет установившееся течение. При этом, как легко видеть, по мере нарастания пограничного слоя на начальном участке должно изменяться и движение во внешнем потоке. Таким образом, начальный участок дает нам пример существенного взаимного влияния пограничного слоя и внешнего потока.

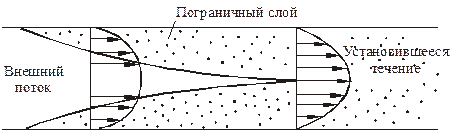
Рис. 1.4. Пограничный слой на входе в трубу


Струя жидкости, вытекающей в пространство, заполненное другой жидкостью, также является примером пограничного слоя (рис. 1.5). Процесс смешения в этом случае также происходит в вязком пограничном слое.

Рис. 1.5. Истечение струи в пространство (затопленная струя)

Как известно, течение в канале или в пограничном слое может быть ламинарным или турбулентным. В технических устройствах преобладающая часть движений происходит при весьма больших числах Re и эти движения являются турбулентными. Поэтому в нашем курсе основное внимание будет уделено анализу турбулентных течений. Кроме того, следует иметь в виду, что для ламинарного пограничного слоя может быть выписана замкнутая система дифференциальных уравнений. Для турбулентного же пограничного слоя эта система не замкнута. Поэтому задачи ламинарного пограничного слоя могут быть решены теоретически, и если получение их решений ограничено, то только математическими трудностями. Для замыкания же системы уравнений турбулентного пограничного слоя приходится строить те или иные физико-математические модели.

Ниже мы рассмотрим некоторые методы решения задач ламинарного пограничного слоя, а пока перейдем к упрощению дифференциальных уравнений движения Навье – Стокса.

1.5.   Дифференциальные уравнения пограничного

         слоя (УРАВНЕНИЯ ПРАНДТЛЯ)

Как уже указывалось, впервые способ упрощения уравнений Навье – Стокса при больших значениях числа Re был предложен Прандтлем в 1904 г. Получаемые при этом дифференциальные уравнения пограничного слоя иногда называют уравнениями Прандтля. При упрощениях уравнений Навье – Стокса принимают, что толщина пограничного слоя намного меньше характерного размера тела, d << L.


Произведем упрощение уравнений Навье – Стокса для случая двумерного несжимаемого потока, обтекающего плоскую пластину (см. рис. 1.1):

,                    (1.18)

.                     (1.19)

.                                      (1.20)

Входящие в эти уравнения параметры U, V, p представляют собой мгновенные (полные) значения скорости и давления. Если течение ламинарно, то мгновенные значения суть средние. Упрощение системы уравнений Навье – Стокса производится на основании оценки порядка величин отдельных членов, входящих в уравнения, и отбрасывания малых. Но количественное сравнение различных величин возможно только в том случае, если они представлены в безразмерной форме.

Перепишем уравнения (1.18)…(1.20) в безразмерной форме, для чего все скорости отнесем к скорости набегающего потока U0, а все длины – к характерному размеру тела L, который выберем так, чтобы порядок безразмерной величины   не превышал единицы. Давление р сделаем безразмерным, разделив его на динамический напор .

Безразмерные величины примут вид

;       ;       ;

;         ;          ;         .

Здесь штрих обозначает безразмерную величину. Подставим в уравнения (2.18)…(1.20) безразмерные величины и получим

;               (1.21)

1    1            1        1      

;                (1.22)

1         1                           

= 0.                                        (1.23)

                                   1         1

Оценка порядка величин.  Для выяснения сущности оценки рассмотрим простой пример. Если какая-то величина z изменяется от 0 до z0, то говорят, что  zпорядка z0.

Поскольку в нашем случае продольная скорость изменяется от U = 0 на стенке до U = U0 на внешней границе пограничного слоя, а продольная координата х от нуля до L, их безразмерные величины U¢и  х¢  будут порядка 1.

Скачать файл