Основные законы движения жидкости и газа, страница 12

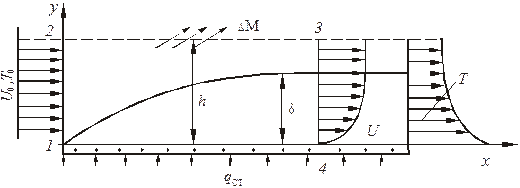
Рис. 1.9. К выводу уравнения энергии балансовым

методом

Выделим  контрольный объем жидкости сечениями 1-2 и 3-4, кроме того, проведем контрольную поверхность, параллельную стенке, на высоте h> d ~ d_т, большей толщины пограничного слоя. Составим баланс тепловой энергии для рассматриваемого объема. Ширина этого объема в плоскости, перпендикулярной рисунку, рав-на единице. DМ – масса жидкости, вытекающей из контура за счет того, что расход через сечение 3-4 меньше расхода через сечение 1-2.

Приравниваем количество теплоты, поступающей в контур, к количеству уносимой теплоты:

.              (1.70)

Масса жидкости, вытекающей из контура за счет подтормаживания силами трения:

.                               (1.71)

Соответственно имеем

;

                               (1.72)

или

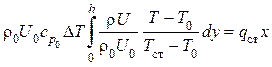;                      (1.73)

при этом . Тогда, дифференцируя выражение (1.73), имеем

,  

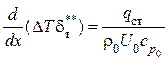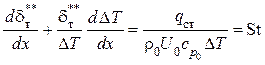.                  (1.74)

Как видим, уравнение (1.74) полностью совпадает с уравнением (1.65) для обтекания плоской непроницаемой пластины безградиентным потоком, т.е. при

.

Аналогично, применяя к рассматриваемому участку пограничного слоя законы сохранения количества движения и сохранения массы i-го компонента, можно получить интегральные уравнения импульсов и диффузии пограничного слоя.

1.6.5.  Условия замыкания интегральных уравнений

В интегральные уравнения импульсов, энергии и диффузии входят величины , представляющие собой некоторые физические масштабы пограничного слоя. Удобство использования указанных величин в качестве масштабов заключается  в том, что в отличие от толщины пограничного слоя интегральные толщины – величины вполне определенные, их значения достаточно точно находятся из эксперимента. В этой связи удобно записать характерные числа Re динамического, теплового и диффузионного пограничных слоев в следующем виде:

Если их ввести в соответствующие интегральные соотношения, полученные выше, после несложных преобразований получим:

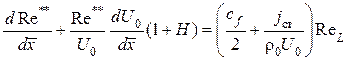;                (1.75)

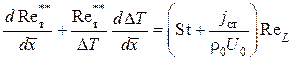;                      (1.76)

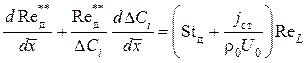,                   (1.77)

где  – число Re, построенное по характерному размеру тела:  – безразмерная координата;  .

Полученные интегральные уравнения могут быть решены, если известны так называемые законы сопротивления, теплообмена и массообмена, которые в общем случае можно представить в таком виде:

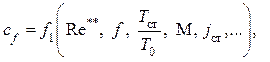f – формпараметр,

.

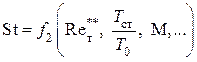Вид этих функций прежде всего зависит от режима течения в пограничном слое. Как будет показано несколько позже, для ламинарного течения законы трения и тепломассообмена можно при определенных граничных условиях получить аналитическим путем. Для турбулентного же режима их получают на основании полуэмпирических теорий турбулентности с привлечением экспериментальных данных.

В дальнейшем будет показано, что законы трения и тепломассообмена, записанные в такой форме, консервативны к изменению граничных условий. Это связано с тем, что они построены по локальным характеристикам пограничного слоя, а не по размерам тела. Полученные для «стандартных условий», т.е. для случая безградиентного обтекания пластины потоком газа с постоянными физическими свойствами, они могут быть использованы и в более сложных условиях. Влияние же разнообразных граничных условий достаточно полно учитывается при интегрировании уравнений импульсов, энергии и диффузии.

Если ввести в правую часть интегральных соотношений (1.75)…(1.77) значения коэффициента трения , теплового  и диффузионного   чисел Стентона, полученных для «стандартных условий», то они примут вид

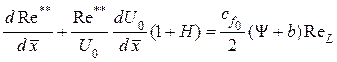;                (1.78)

.                       (1.79)

Здесь – параметр проницаемости стенки, отнесенной к коэффициенту трения в стандартных условиях;  – тепловой параметр проницаемости, отнесенный к числу Стентона в стандартных условиях: – относительный закон трения и  – относительный закон теплообмена при соответственно одинаковых значениях  или .

Эти относительные функции теплообмена учитывают влияние температурного фактора, проницаемости стенки, числа Маха и других возмущающих воздействий по сравнению со стандартными условиями.