Основные законы движения жидкости и газа, страница 11

.

Можно по аналогии с толщиной вытеснения определить толщину потери импульса  как толщину, через которую при течении идеальной жидкости проходило бы количество движения, равное потере количества движения в сечении пограничного слоя за счет тормозящего действия сил трения.

В случае обтекания осесимметричных тел вращения при  интегральное уравнение импульсов имеет вид

,  (1.55)

где  ;  ;

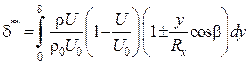R_x – радиус поперечного сечения тела;  b – угол между касательной к меридиану и осью;  х  и  у – оси координат, направленные соответственно: вдоль меридианального сечения  а  и по нормали к профилю. Знак (+) берется при внешнем обтекании, (–) – при внутреннем (рис. 1.8).

Рис. 1.8. Пограничный слой на теле вращения

1.6.2.  ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ЭНЕРГИИ

Интегральные уравнения энергии (и диффузии) пограничного слоя выводятся аналогичным образом. Для этого дифференциальное уравнение энергии

                   (1.56)

преобразуем с помощью уравнения неразрывности

                                    (1.57)

к следующему виду:

.                      (1.58)

Умножим уравнение неразрывности на температуру газа вне пограничного слоя Т₀, которая является постоянной величиной:

.                         (1.59)

В случае течения сжимаемого газа используется температура торможения основного потока. Здесь же для простоты мы рассмотрим течение несжимаемого газа с постоянными физическими свойствами r, с_р, l = const.

Вычтем почленно из уравнения неразрыности уравнение энергии и проинтегрируем поперек пограничного слоя от у = 0 до у = ¥;

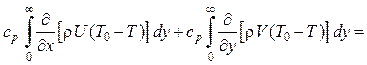
.                         (1.60)

Используя граничные условия:

при   y = 0:   U = 0,      V = V_ст,    r = r_ст,   T = T_ст;

при   y = ¥:  U = U₀,    T = T₀, преобразуем интегралы полученного уравнения (1.60):

,

.

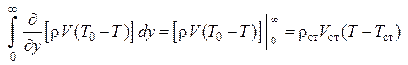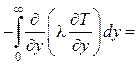
Вводя понятие толщины потери энергии

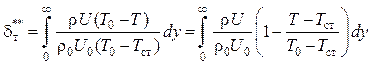,           (1.61)

физический смысл которой ясен из рис. 1.7,б, перепишем интеграл в левой части уравнения (1.60) в следующем виде:

.                       (1.62)

Как и при выводе интегрального уравнения импульсов, считаем, что операции дифференцирования и интегрирования можно поменять местами. Подставляя полученные значения интегралов в исходное уравнение (1.60), получаем

                           (1.63)

или

.

Введя число Стентона

,                                (1.64)

преобразуем уравнение энергии к окончательному виду:

= St .             (1.65)

Если использовать сразу дифференциальное уравнение энергии, записанное через энтальпии, то и интегральное уравнение получим в аналогичной форме, где вместо значений температур будут стоять соответствующие значения энтальпий.

Следует отметить, что интегральное соотношение энергии впервые было получено  Г.Н. Кружилиным.

В случае обтекания осесимметричных тел в интегральное соотношение энергии дополнительно войдет, как и в уравнение импульсов, радиус R_x:

,     (1.66)

где толщина потери энергии с учетом кривизны поверхности

.

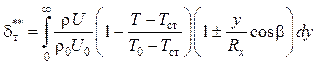1.6.3.   Интегральное уравнение диффузии

Интегрируя уравнение диффузии i-го компонента по сечению пограничного слоя

и учитывая уравнение неразрывности, получаем совершенно аналогичное (1.65) интегральное соотношение диффузии пограничного слоя:

.      (1.67)

Здесь  – разность массовых концентраций i-го ком-понента в основном потоке и на стенке:  ;

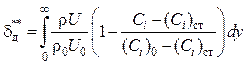                        (1.68)

– толщина потери вещества;   

                          (1.69)

– диффузионное число Стентона. 

1.6.4. Получение  интегральных  уравнений

          балансовым  методом

Интегральные соотношения можно также получить, рассматривая баланс количества движения, энергии и вещества для объема жидкости, выделенного двумя сечениями в пограничном слое. Поскольку при этом не закладывается никаких гипотез о механизме течения (ламинарного или турбулентного), сами интегральные уравнения импульсов, энергии и диффузии справедливы как для ламинарного, так и для турбулентного течения в пограничном слое.

Составление интегральных соотношений балансовым методом является очень наглядным. Рассмотрим это на примере уравнения энергии для простейшего течения газа с постоянными физическими свойствами вдоль плоской стенки в случае подвода теплоты к стенке по закону q_ст = const ¹ f(x) (рис. 1.9).