Основные законы движения жидкости и газа, страница 9

Здесь следует обратить внимание на то, что при упрощениях полных дифференциальных уравнений энергии и диффузии можно оценить порядок толщины теплового и диффузионного слоев. Поясним это на примере уравнения энергии. После приведения к безразмерному виду имеем:

.                     (1.34)

Здесь – безразмерная температура.

В этом случае в правой части появляется новый безразмерный критерий, называемый числом Пекле,

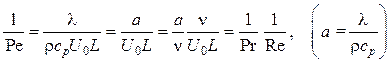
и равный произведению Ре = RePr = U₀L/a. Число Пекле представляет собой некоторый тепловой аналог числа Рейнольдса, характеризующий соотношение конвективного переноса теплоты и переноса теплоты теплопроводностью.

Если теперь произвести оценку порядка членов в уравнении энергии (1.34), как это делалось с уравнениями движения, то увидим, что перенос теплоты вследствие  теплопроводности (в правой части) будет одного порядка с переносом теплоты конвекцией (слева), если

;    .                       (1.35)

Сравнив (1.35) с соотношением (1.27) для толщины динамического слоя, получим

.                                         (1.36)

Это выражение дает наглядное толкование влияния числа Прандтля. Оно показывает, что в газах толщина теплового пограничного слоя близка к толщине динамического, так как для газов число Pr близко к единице, в жидкостях же (Pr = 10…1000, см. табл. 1.2) тепловой слой тоньше динамического.

Аналогичное соотношение можно получить и для толщины диффузионного слоя:

.                                          (1.37)

Выше приведены рассуждения для стационарных течений. Почти все потоки, встречающиеся в технике, с достаточной степенью точности можно считать стационарными.

Для нестационарного течения уравнение движения имеет вид

.           (1.38)

Количественная оценка квазистационарности течения в пограничном слое может быть сделана путем сравнения первого члена этого уравнения со вторым. Скорость U  имеет порядок U₀, градиент скорости

   а  .

Первым членом в уравнении (1.38) можно пренебречь, если

.

       или                                   (1.39)

Для тела размером L = 0,3 м, обтекаемого потоком со скоростью U₀ = 30 м/с, течение можно рассматривать как квазистациорнарное, когда изменения в нем имеют место за период времени, больший, чем L/U₀ = 0,01 с. Если же изменения происходят за меньший промежуток времени, то течение рассматривают как нестационарное. Изменения течений за такое короткое время встречаются редко. Поэтому в дальнейшем мы будем рассматривать стационарные течения.

1.6.  ИНТЕГРАЛЬНЫЕ СООТНОШЕНИЯ

        ПОГРАНИЧНОГО СЛОЯ

Полученные дифференциальные уравнения пограничного слоя проще соответствующих полных дифференциальных уравнений движения, энергии и диффузии вязкой жидкости. Тем не менее точное решение системы дифференциальных уравнений пограничного слоя возможно лишь для ограниченного круга задач с достаточно простыми граничными условиями, когда дифференциальные уравнения пограничного слоя в частных производных могут быть сведены к обыкновенным дифференциальным уравнениям. Примером может служить рассмотренное выше решение Блазиуса для плоской стенки.

Для решения более общих задач применяют численные методы. Однако процесс расчета зачастую становится громоздким и трудоемким. В этой связи большое значение приобретают приближенные методы решения указанных уравнений, основанные на при-менении так называемых интегральных соотношений импульсов, энергии и массы. Интегральные соотношения получают в результате интегрирования дифференциальных уравнений движения, энергии и диффузии по толщине пограничного слоя. Интегральные уравнения пограничного слоя являются балансовыми для рассматриваемого сечения пограничного слоя и по структуре точными, по крайней мере, в рамках теории пограничного слоя. Приближенный характер решения этих уравнений обусловлен способом их замыкания.

Метод интегральных соотношений отличается большой простотой, и во всех случаях разумного применения он дает удовлетворительные результаты.

1.6.1.  Интегральное соотношение импульсов