Интегральное уравнение количества движения (импульсов) получают из дифференциальных уравнений движения и неразрывности
![]() ,
(1.40)
,
(1.40)
![]() (1.41)
(1.41)
с помощью интегрирования по толщине пограничного слоя. Это уравнение выражает закон сохранения импульса жидкости, протекающей через данное сечение пограничного слоя.
Уравнение движения (1.40) с учетом
уравнения неразрывности (1.41) и уравнения Бернулли для градиента давления ![]() =
= ![]() можно
представить в следующей форме:
можно
представить в следующей форме:
![]() .
(1.42)
.
(1.42)
Умножив все члены уравнения неразрывности (1.41) на значение скорости на внешней границе пограничного слоя U0, получим
![]() , (1.43)
, (1.43)
при этом учтено, что
![]() и
и ![]() .
.
Вычитая почленно из уравнения (1.43) выражение (1.42), получаем
![]() . (1.44)
. (1.44)
Проинтегрируем теперь каждый член преобразованного уравнения движения (1.44) поперек пограничного слоя:

 .
(1.45)
.
(1.45)
Допуская возможность замены порядка дифференцирования и интегрирования при бесконечном верхнем пределе, получаем
![]()
![]() .
(1.46)
.
(1.46)
Будем здесь рассматривать общий случай обтекания проницаемой стенки, когда значение поперечной скорости на ней отлично от нуля (рис. 1.6).
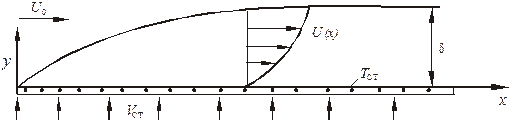
Рис. 1.6. Пограничный слой на проницаемой пластине
Стенка является проницаемой. Такая постановка задачи имеет место при пористом охлаждении поверхности, при испарении или конденсации на стенке, на выгорающей поверхности. Во всех этих примерах на стенке существует поперечный поток вещества, т.е. (rV)ст ¹ 0. При этом граничные условия принимают вид:
при у = 0: U = 0, V = Vст, r = rст, t = tст;
при у = 0: U = U0, r = r0, ![]() , t = 0. (1.47)
, t = 0. (1.47)
Тогда отдельные члены уравнения (1.46) можно представить в виде
![]() ;
; ![]() ;
(1.48)
;
(1.48)
![]()
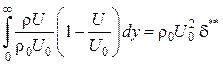 ;
(1.49)
;
(1.49)
![]()
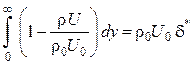 .
(1.50)
.
(1.50)
Верхний предел интегрирования в выражениях (1.49) и (1.50) может быть заменен толщиной пограничного слоя (так как выше нее интегралы равны нулю), тогда выражения для толщины вытеснения и толщины потери импульса принимают вид
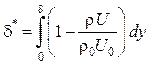 ;
;  .
(1.51)
.
(1.51)
(Ниже мы вернемся к этим важным параметрам и дадим их физическое толкование.)
Подставляя полученные выражения (1.48)…(1.50) в уравнение (1.46), получаем интегральное соотношение импульсов пограничного слоя (его иногда называют уравнением Кармана, впервые получившим его):
![]() .
(1.52)
.
(1.52)
При обтекании несжимаемой жидкости r0 = const после раскрытия производной уравнение импульсов принимает вид
![]() .
(1.53)
.
(1.53)
Уравнению импульсов иногда придают другие формы записи, как, например:
![]() .
(1.54)
.
(1.54)
Здесь ![]()
![]() – формпараметр
пограничного слоя;
– формпараметр
пограничного слоя;![]() –
формпараметр, характеризующий аэродинамическую кривизну обтекаемого тела.
–
формпараметр, характеризующий аэродинамическую кривизну обтекаемого тела.
Толщина вытеснения ![]() и толщина
потери импульса
и толщина
потери импульса ![]() являются
важными расчетными характеристиками пограничного слоя. Интегральные
характеристики типа
являются
важными расчетными характеристиками пограничного слоя. Интегральные
характеристики типа ![]() и
и
![]() обладают тем
замечательным свойством, что увеличение верхнего предела интегрирования у
> d практически не изменяет их значения.
При экспериментальном определении с достаточно аккуратными измерениями такие
характеристики пограничного слоя практически не чувствительны к дальнейшему
увеличению точности приборов, в то время как значение толщины пограничного слоя
прямо связано с выбором значения
обладают тем
замечательным свойством, что увеличение верхнего предела интегрирования у
> d практически не изменяет их значения.
При экспериментальном определении с достаточно аккуратными измерениями такие
характеристики пограничного слоя практически не чувствительны к дальнейшему
увеличению точности приборов, в то время как значение толщины пограничного слоя
прямо связано с выбором значения ![]() .
.
Иначе говоря, для пограничного слоя можно записать
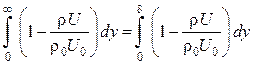 .
.
Из равенства
![]()
следует, что толщину вытеснения можно
определить как некоторую часть толщины пограничного слоя (рис. 1.7,а),
через которую секундный массовый расход идеальной жидкости равен потере расхода
через пограничный слой за счет тормозящего действия сил трения. Как видно
из рисунка, толщина вытеснения ![]() ,
в отличие от толщины пограничного слоя d, – величина вполне определенная.
,
в отличие от толщины пограничного слоя d, – величина вполне определенная.
|
|
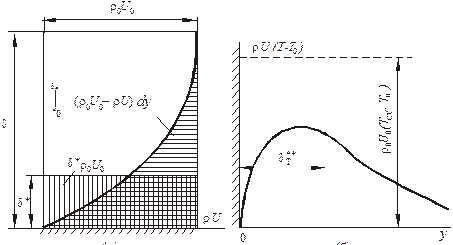
а б
Рис. 1.7. К определению толщины вытеснения (а)
и толщины потери энергии (б)
Перепишем выражение для толщины потери
импульса ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.