Здесь множество индексов Оо отвечает общим для модели ограничениям, а остальные множества Од — локальным ограничениям отраслей.
Допустим для простоты, что области, определяемые неравенствами (129) ограничены. Пусть векторы ^^{Z^i^Ok - вершины многогранников,' отвечающих локальным ограничениям отрасли &. Любой допустимый план отрасли является выпуклой комбинацией Z^, т. е.

В этих обозначениях задача центрального органа по методу Данцига— Вулфа может быть сформулированав виде
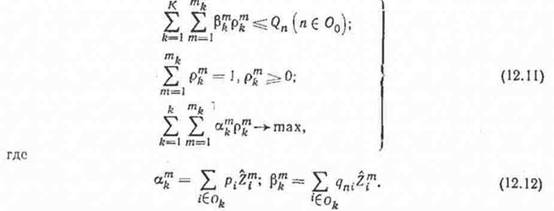
Искомые величины р^ в задаче (12.11) имеют смысл интенсивностей использования опорных планов Z^ в каждой из отраслей.
Решению задачи (12.11) соответствуют двойственные оценки ограничений Эп, п^Оо, которые сообщаются отраслям и служат для корректировки локальных планов.
Локальная подзадача отрасли при этом имеет вид
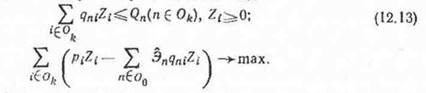
Второе слагаемое в целевой функции можно интерпретировать как плату аа ресурсы.
Решения локальных подзадач на следующем шаге используются для построения целевой функции и ограничений центральной задачи в соответствии с определением (1211). Существует достаточно простой алгоритм, позволяющий за конечное число шагов либо найти оптимальное решение исходной задачи, либо убедиться в несовместности ее условий. Заметим, что в общем случае нет необходимости проводить на каждом шаге локальную оптимизацию во всех подзадачах; важно только, чтобы очередной вариант распределения планов и оценки общих ресурсов были «лучше» (в смысле глобального критерия), чем предыдущие.
В подходе Корнай—Липтака центральный орган выделяет каждой отрасли некоторые объемы общих ресурсов Од (пб Оо)- После этого решаются локальные задачи с учетом ограничений по всем ресурсам:
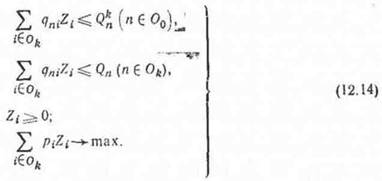
Такая задача отвечает стремлению каждой отрасли как можно эффективнее использовать выделенный ей объем общих ресурсов. Двойственные оценки соответствующих ограничений этих задач характеризуют эффективность выдвинутого центром варианта распределения ресурсов. Получив эти оценки, центр корректирует распределение ресурсов, решая задачу
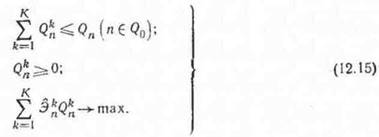
Как видно, задача (12.15) распадается на Л/о (где No—число видов общих ресурсов) не связанных между собой задач распределения ресурса п (/i60o), в каждой из которых имеется единственное связывающее ограничение. Решение такой задачи имеет весьма простои экономический смысл и состоит в том, что весь запас ресурса п выделяется тон отрасли, для которой оценка эффективности использования этого ресурса максимальна. Если же несколько отраслей используют данный ресурс с равной эффективностью, то его можно выделить в любой из этих отраслей.
Аппроксимация. В простейших алгоритмах декомпозиции, рассмотренных выше, неявно содержится идея аппроксимационного подхода к построению многоуровневой системы синтеза. Она состоит в аппроксимации производственных возможностей хозяйственного объекта с помощью одного ограничения. Действительно, в методе Данцига—Вулфа центральный орган опе303
рирует опорными планами отраслей, предполагая, что множество допустимых планов для каждой отрасли задается выпуклой оболочкой опорных планов.
В общем случае допустимые опорные планы на первом шаге могут выбираться достаточно произвольно. При этом множество производственных возможностей (допустимых планов) будет описываться приближенно. На каждом шаге итерации получают новый допустимый план, который можно использовать для уточнения аппроксимации.
Аппроксимационный подход позволяет принять довольно естественную схему агрегирования, в которой производственные возможности отраслей характеризуются укрупненными показателями.
Пусть целевая функция и ограничения исходной "задачи (12.8) зависят только от агрегированных переменных 2ft=SZ,.
^°* Тогда на каждой итерации центральный орган составляет проект плана {2.^} в агрегированных показателях и передает его отраслям. Отрасли, руководствуясь критерием минимального отклонения укрупненного показателя Z/, от варианта, предложенного центром, составляют альтернативные планы как в укрупненных, так и в детализированных показателях. При этом в результате решения локальных задач вырабатываются оценки укрупненных планов центра, например по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.