При существенном влиянии транспортного фактора в качестве неизвестных выступают интенсивности объемов поставок продукции от предприятий-поставщиков к потребителям. Задача планирования производства рассматривается как" производственно-транспортная. К этому классу относятся, например, производство цемента, проката черных металлов, минеральных удобрений, сельскохозяйственной продукции и т. д.
Рассмотрим, следуя в основном В. А. Волконскому, общую схему синтеза отраслевой модели.
Пусть отрасль объединяет ! предприятий (подотраслей, объектов'), и на каждом предприятии можно реализовать один или несколько из fif[j=\, .^технологических способов производства. Будем считать, что определено понятие весового коэффициента р^ использования способа k на предприятии / (^=1, 2, ...» п.,). Если р^==0,то способ вовсе не используется, при р== 1 предприятие /' работает только по способу k. Таким образом,
![]()
Некоторые способы могут использоваться с любым значением коэффициента 0 ss р? ^ 1 (например, при составлении плана перевозок pf —доля поставок предприятия / в пункт k}.
При составлении отраслевого плана необходимо учитывать балансовые ограничения, налагаемые на производство и потребление различных продуктов и ресурсов. Интенсивность производства (потребления) продукта ( ((==1, 2,...,/) на предприятии /, которую мы обозначаем через Zij, зависит от р/, т.е.
![]()
Иногда для удобства записи принимают, что если ^-^О, то продукт производится, если Z^O, то он потребляется. Тогда балансовые ограничения для отрасли имеют вид
![]()
где Qi — потребность потребителей в продукте i или (взятый со знаком минус) лимит внешних ресурсов.
Допустимым отраслевым планом называется совокупность величин pj или соответственно Z,;, удовлетворяющая условиям
(12.18)—(12.20). а также требованиям целочнсленности р?, если таковые имеются.
Задача оптимального отраслевого планирования состоит в отыскании такого плана среди всех допустимых, который доставляет экстремум целевой функции С/(р) или U(Z).
Описанную выше модель можно понимать и как статическую. и как динамическую. В последнем случае значения некоторой величины в разные моменты времени рассматривают как переменный параметр.
Для практических расчетов необходимо располагать в явном виде функциями f,} и U. Хотя существование оптимального решения и ряд его важных свойств установлены для достаточно широкого класса этих функций, вычислительные трудности заставляют в большинстве случаев ограничиваться простейшими предположениями об их структуре. В дальнейшем будем рассматривать только линейные отраслевые модели, т. е. считать, что
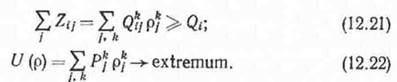
При этом P^s можно интерпретировать, например, как прибыль (или взятые со знаком минус затраты) от работы предприятия / по способу k с единичной интенсивностью, а интерпретация ресурса q.ij зависит от конкретного характера задачи.
В практике оптимального отраслевого планирования в качестве критерия оптимальности чаще всего принимается либо максимум суммарной прибыли при наличии ограничений на затраты дефицитных ресурсов и заданных минимальных уровнях потребления конечной продукции отрасли, либо минимум суммарных затрат при тех же ограничениях. Иногда уровень потребления фиксируется, и часть неравенств (12.21) обращается в равенства.
Критерий минимума затрат целесообразен при выполнении хотя бы одного из следующих условий: 1) спрос на продукцию практически не зависит от цен реализации и подлежит обяза307
тельному удовлетворению; 2) цены на продукцию не могут быть установлены к моменту решения задачи; 3) прогнозы лимитов на дефицитные ресурсы менее надежны, чем прогнозы спроса.
Критерий максимума прибыли целесообразно использовать в следующих случаях: 1) спрос на продукцию существенно зависит от цены ее реализации; 2) потребность в продукции не может быть полностью удовлетворена предприятиями отрасли;
3) ассортиментная структура производимой продукции не может быть заранее задана и подлежит определению в процессе решения задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.