Задачи планирования в условиях риска с неполной информацией о статистических характеристиках управляемого объекта обычно формулируются как стохастические экстремальные задачи. Подходы к их постановке и решению существенно различаются в зависимости от того, получают ли информацию об условиях задачи всю сразу или «порциями», с разрывом во времени, а также от того, необходимо ли принять единственное решение, не подлежащее корректировке, или его можно корректировать по мере накопления информации. В первом случае говорят о статической, или одноэтапной, задаче, во втором — о динамической, или многоэтапной, задаче стохастического программирования.
Стохастические модели особенно полезны для оптимизации систем, в которых существенно взаимодействие процессов спроса и предложения. Балансовые отраслевые модели рассмотренного выше типа здесь оказываются практически непригодными: условия межпродуктового внутриотраслевого баланса в таких случаях, как правило, отсутствуют, а внешние ограничения носят четко выраженный вероятностный характер.
Приведем в качестве примера задачу о заготовках и реализации сельскохозяйственной продукции. Для простоты рассмотрим однопродуктовую модель с одним поставщиком и одним потребителем.
Пусть сезон заготовок разбит на Т временных интервалов, и необходимо составить план, определяющий объем заготовок в каждом из этих интервалов с учетом спроса населения на продукцию и ожидаемой урожайности.
В балансовой модели основным ограничением было бы условие, что планируемый объем заготовок в каждом интервале времени не должен превышать размера ожидаемого урожая. В стохастической задаче аналогом такого ограничения будет условие, что вероятность выполнения составленного плана должна быть не меньше определенной величины.
Пусть известна плотность распределения вероятностей для ожидаемого урожая в интервале времени /, равная р^ (г). Тогда вероятность выполнения (или перевыполнения) плана z» есть
![]()
я если мы требуем, чтобы вероятность выполнения плана была йе меньше а, то
![]()
Далее, спрос населения в интервале времени t также случайная величина с плотностью распределения вероятностей qt(D). В первом приближении величины г и D статистически независимы.
Заметим, что при любом плане, удовлетворяющем ограничениям (1236), не исключена возможность как возникновения дефицита (т. е. превышения спроса над фактическим объемом заготовок), так и образования излишков заготовленной продукции. При этом экстремальную стохастическую задачу можно сформулировать, например, как задачу минимизации вероятности возникновения дефицита или математического ожидания дефицита. Можно также каким-то образом рассчитывать издержки, связанные с возникновением дефицита или излишков продукции, и включать эти издержки в целевую функцию. „
Распределение вероятностей возникновения дефицита в такой модели имеет вид
![]()
Аналогично для распределения излишков имеем
![]()
Постановка задачи отыскания плана заготовок, минимизирующего математическое ожидание излишков, при условии, что вероятность возникновения дефицита не превысит Р *, будет включать ограничение
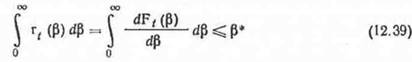
в целевую функцию:

Вообще говоря, заготавливаемая продукция может быть реализована не сразу, а сохранена для создания резервного запаса. Поэтому стратегия управления запасами в каждый момент времени будет зависеть как от статистической априорной информации об уровнях ожидаемого урожая и спроса p<(z) и qt(D), так и от достоверной информации о текущем уровне запасов продукции. Тогда соответствующая задача будет существенно динамической, или многоэтапной.
12.4. Материальное обеспечение производства
Синтез хозяйственных связей. В 10.2. уже говорилось о системе материальных, межпродуктовых и межотраслевого балансов как основе разработки планов распределения продукции про314
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.