где (fni—затраты ресурса вида п на единицу продукции вида ц для простоты предположим, что ограничения модели Qn выражают как лимиты по использованию дефицитных ресурсов, так и предельные (или фиксированные) задания по конечному выпуску продукции. В дальнейшем это обстоятельство не будет оговариваться специально, и все ограничения модели (12.8) будем называть ограничениями на использование дефицитных ресурсов.
В реальной экономике далеко не каждый из N видов ресурсов используется для производства продукции в каждой из отраслей, поскольку имеются ресурсы, используемые единственной или немногими отраслями. Кроме того, ограничения в модели (12.8) включают и предельные задания по выпуску продукции, а каждый продукт, ьак было определено, производится только одной отраслью. Следовательно, по крайней мере часть ограничений модели (12.8) относится только к какой-то конкретной отрасли.
В этом случае исходная задача оптимизации приобретает так называемую блочную структуру, при которой матрица ограничений имеет примерно следующий вид:

Здесь верхняя строка соответствует общим для модели (12.8) ограничениям (например, лимитам по использованию общих
300
для всех отраслей ресурсов). Остальная часть матрицы легко } разбивается на блоки, соответствующие различным отраслям.
Такая структура матрицы создает естественные предпосылки для построения двухуровневой системы планирования с разбиением (декомпозицией) исходной задачи на ряд локальных подзадач (в пределах каждого блока) и одну координирующую (центральную) задачу, функция которой состоит в отыскании согласованного решения. Можно предложить два различных подхода к планированию в такой системе.
При первом подходе центральный орган планирования осуществляет координацию путем установления оценок («цен») на продукцию (или ресурсы). В соответствии с этими оценками каждая отрасль строит свой вариант оптимального плана, максимизирующий «прибыль» (или минимизирующий издержки) с учетом установленных оценок и ограничений по ресурсам. При этом суммарнын план всей системы оказывается несогласованным. Центральный план изменяет оценки продукции (ресурсов) так, чтобы уменьшить эти невязки, оценки недостающей продукции (перерасходованных ресурсов) увеличиваются, а излишней продукции (сэкономленных ресурсов) — уменьшаются. В результате за конечное число шагов удается достичь точного или приближенного (в зависимости от способа корректировки оценок) решения исходной задачи.
Второй подход основан на выдвижении центральным органом некоторого варианта плановых заданий по выпуску продукции или использованию ресурсов для каждой из отраслей так, чтобы обеспечить выполнение ограничений модели в целом. На основе этих заданий каждая отрасль составляет свой план использования наличных ресурсов так, чтобы минимизировать общие издержки производства (максимизировать прибыль), а цены (глобальные оценки) в данном случае предполагаются фиксированными. При этом издержки, приходящиеся на единицу каждого вида продукции (или оценки использования общих ресурсов), служат оценками предложенного варианта распределения плановых заданий (ресурсов) и сообщаются в центральный орган. Пользуясь этими оценками, центр разрабатывает новый вариант распределения планов и т. д.
Следовательно, в обоих подходах согласованное решение достигается путем «диалога» центрального и периферийных плановых органов по показателям «план—оценка». При этом оба рассмотренных подхода по отношению друг к другу выступают как дополнительные. Л именно, в первом подходе информационные связи между центром и периферией строятся по схеме «глобальные оценки — план», во втором — по схеме «план—локальные оценки». Наиболее известным алгоритмом для реализации первого подхода в задачах линейного программирования является метод Данцига — Вулфа, а второго — метод Корнай— Липтака.
301
Рассмотрим методы Данцига—Вулфа и «Корнаи—Липтака подробнее. Для этого условия исходной задачи (12.8-) следует описать более детально выделив явно общие для всех отраслей ограничения: '
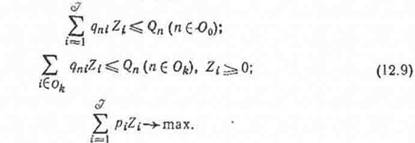
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.