Многоуровневый синтез и реализация плана (Глава учебного пособия "Экономическая кибернетика"), страница 7

Эта проблема сводится к решению системы К уравнений

. Очевидно, что система (12.2) значительно проще (12.1). так как K<J. Но для того чтобы определить элементы матрицы [оа(], необходимо знать веса р^, значения которых определяются в результате решения системы (12.1).

Поскольку pj заранее не известны, можно пытаться строить агрегированные показатели эмпирически на основе предшествующего опыта. При этом, однако, неизбежно возникают ошибки агрегирования, связанные с неточными значениями р;.

В некоторых частных случаях условие точного агрегирования может быть выполнено, но исследователи ищут более общие, хотя и приближенные, решения этой проблемы, чтобы по возможности уменьшить возникающие в процессе агрегирования ошибки. Разработанные в СССР методы итеративного агрегирования позволяют построить такой процесс последовательных

298

Приближений, который реализует многоуровневую схему планирования с агрегационной структурой.

Идею метода итеративного агрегирования удобно пояснить непосредственно на примере рассмотренной выше балансовой задачи (12.1), (12.2).

Начальный этап итерационного алгоритма состоит в выборе некоторого (вообще говоря, произвольного) вектора полного выпуска продуктов в детализированной номенклатуре (^ }• На основе значений Z ? рассчитываются объемы выпуска агрегированных продуктов отраслей: Z^ = Vz^ и межотраслевые потоки затрат;

где М ^⁾ — полуагрегированный поток затрат продукта детализированной номенклатуры па агрегированный продукт отрасли I:

С помощью величин Mki агрегированную систему уравнений МОБ можно переписать в более удобном для итерационной схемы виде. Здесь неизвестными являются уже не объемы выпуска агрегированных продуктов отрасли, а величины их изменения S»i на данной итерации по сравнению с предыдущей. Иначе, если на итерации г были получены значения объемов Zy, то на итерации г+1 будут приняты значения

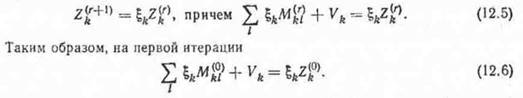
Полученные в результате решения системы (12.6) значения ^ используются для дезагрегирования объемов выпуска продукции и получения нового приближения для переменных детализированной номенклатуры, исходного для следующей итерации:

где Vf^ ^решение системы (12.6).

Анализ сходимости такого процесса показал, что он сходится для достаточно широкого класса матриц затрат [о<Л. Во всяком случае, сходимость обеспечена для задачи стоимостного МОБ 2а^<1.

Даже такая простая схема итеративного агрегирования содержит «зародыш» многоуровневой схемы управления. Действительно, центральный планирующий орган в данном случае может решать только задачу (12.5) в агрегированных показателях и передавать отраслевым подсистемам найденные значения коэфифциентов ^⁺¹⁾. На основе этой информации отрасль k подсчитывает значения М. ^^'^Г1) я передает эти значения отрасли l(l<=.0i). После обмена информацией отраслевые подсистемы заканчивают решение задачи дезагрегирования в соответствии с (12.7)—каждая для своей группы продуктов. Найденные значения Z^⁴'¹¹ используются для вычисления Z^ '¹⁾ и Z^y ⁾, которые отрасль / передает в центральный планирующий орган для решения задачи межотраслевого баланса на новой итерации.

299

Более сложные алгоритмы итеративного агрегирования используются в оптимизационных моделях, в которые наряду с системой балансовых уравнений типа (12 1) входят ограничения на использование дефицитных ресурсов и целевая функция, выраженные через переменные детализированной номенклатуры. Здесь, помимо агрегирования всех показателей, необходимо выработать способ согласования целевых функций агрегированной и локальных задач, решаемых периферийными органами. Если же эти целевые функции оставить без изменения, сходимость итеративного агрегирования может быть нарушена из за того, что начиная с какого-то момента решения агрегированной задачи будут давать при дезагрегировании недопустимые (с точки зрения ограничении локальных задач) значения детализированных переменных.

Декомпозиция. Рассмотрим схему оптимизации плана как задачу линейного программирования: