a=0,05;
b=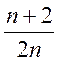 ;
;
n=2 - число осей под одним концом вагона;
fст - статический прогиб рессорного подвешивания;
v=55,6 м/с - скорость движения.
Подставив значения в выражение (1.1), получим значение коэффициента вертикальной динамики Kдв = 2,16.
3.2.1.2. Продольная нагрузка
Продольная нагрузка вычисляется по формуле:
![]() , (1.2)
, (1.2)
где ax - нормированная величина продольного ускорения агрегата.
Для пассажирских вагонов применительно к внутреннему оборудованию ускорение составляет:
- по первому режиму: ax = 5g = 49,1 м/с2;
- по третьему режиму: ax = 2g = 19,6 м/с2.
Для расчетов на прочность выберем первый режим, как более жесткий.
3.2.1.3. Боковая нагрузка
Величина боковой нагрузки задается по формуле:
![]() , (1.3)
, (1.3)
где ax - нормированная величина бокового ускорения агрегата, равная:
- по первому режиму: ay = 0;
- по третьему режиму: ay = 0,4g = 3,92 м/с2.
Для дальнейших расчетов будем использовать значение ускорения из третьего режима.
3.2.1.4. Аварийный режим
Рассмотрим также аварийный режим нагружения агрегатов, соответствующий падению вагона на бок. Этот режим характеризуется внезапным приложением в боковом направлении силы тяжести агрегата.
В этом случае нагрузки могут почти достигать величин, вдвое превышающих силу тяжести. Таким образом, будем рассматривать аварийное действие на агрегаты в боковом направлении нагрузок, равных:
![]() . (1.4)
. (1.4)
3.2.2. Определение опорных реакций
При вычислении опорных реакций в зонах крепления агрегатов составляются уравнения равновесия агрегата, а для статически неопределимых систем - условия совместности деформаций [2]. Используются методы сопротивления материалов и строительной механики.
3.2.3. Оценка прочности элементов крепления
Оценка прочности элементов крепления производится путем определения напряжений методами сопротивления материалов [2] и их сравнения с допускаемыми напряжениями. При этом также учитываются рекомендации "Норм" [1] как по самой методике расчета элементов крепления, так и по значениям допускаемых напряжений.
Приведем формулы для оценки прочности наиболее типичных элементов.
3.2.3.1. Прочность болтовых соединений
При расчете болтовых соединений после определения усилий, действующих на болт, будем оценивать прочность на растяжение, срез и смятие. Это соответствует случаю, когда болты установлены без зазора.
Значения допускаемых напряжений будем принимать в соответствии с "Нормами" по первому режиму.
Напряжения при растяжении оцениваются по формуле:
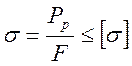 , (1.5)
, (1.5)
где Pp - растягивающее усилие;
F - площадь поперечного сечения болта;
[s] = 195 МПа - допускаемые напряжения при растяжении.
Напряжения среза:
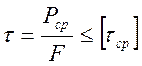 , (1.6)
, (1.6)
где Pср - поперечное усилие;
[tср] = 165 МПа - допускаемые напряжения среза.
Напряжения в болте при смятии:
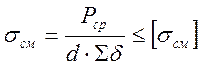 , (1.7)
, (1.7)
Sd - наименьшая суммарная толщина соединяемых элементов, сминаемых в одном направлении.
[sсм] = 360 МПа - допускаемые напряжения смятия.
3.2.3.2. Расчет балок на прочность с применением МКЭ
При расчете статически неопределимых систем применяется метод конечных элементов в форме метода перемещений [3]. Принцип метода состоит в том, что исследуемая конструкция представляется как набор конечных элементов, деформацию которых описать более просто. Элементы стыкуются в узлах. Условием стыковки является равенство узловых перемещений стыкующихся конечных элементов.
При расчете балок конечный элемент выбирается в виде стержня, а геометрические соотношения (зависимости деформаций от перемещений) и физические соотношения (зависимости внутренних усилий от деформаций) примем с использованием гипотезы плоских сечений.
Аппроксимацию перемещений в пределах конечного элемента примем в виде полинома. Для продольного перемещения (при расчете на растяжение-сжатие) используется полином первой степени (линейная аппроскимация), а для поперечных перемещений (при изгибе) - полином третьей степени, который позволяет обеспечить неразрывность в узлах не только перемещения, но и угла поворота в соответствующей плоскости.
Матрица жесткости стержневого конечного элемента при расчете на растяжение-сжатие имеет вид:
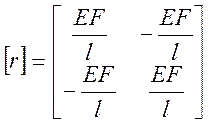 .
.
При расчете на изгиб матрица жесткости имеет вид:
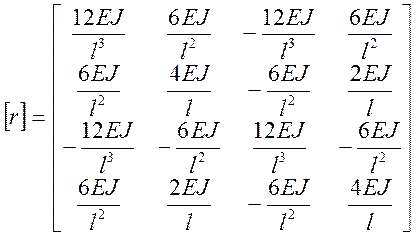 .
.
Разрешающая система уравнений составляется на основе принципа Лагранжа и формируется из вкладов от каждого конечного элемента. После формирования системы уравнений в ней реализуются граничные условия. При заданных нулевых перемещениях в узлах (например, в случае жесткой заделки) из системы уравнений исключаются те строки и столбцы, которые соответствуют нулевым перемещениям.
Из решения системы уравнений определяются узловые перемещения, на основе которых вычисляются внутренние усилия во всех элементах конструкции. Окончательно после определения усилий находятся нормальные напряжения, которые сравниваются с допускаемыми.
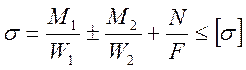 , (1.8)
, (1.8)
где M1, M2 - изгибающие моменты в двух взаимно перпендикулярных плоскостях;
N - усилие растяжения-сжатия в балке;
W1, W2 - моменты сопротивления при изгибе в двух взаимно перпендикулярных плоскостях, соответствующие моментам M1 и M2;
F - площадь поперечного сечения балки.
[s] = 276 МПа - допускаемые напряжения растяжения-сжатия, принимаемые на основании "Норм" [1] по первому режиму.
Расчеты по методу конечных элементов ведутся в матричной форме с применением ЭВМ.
Расчетные схемы крепления вентиляционного короба

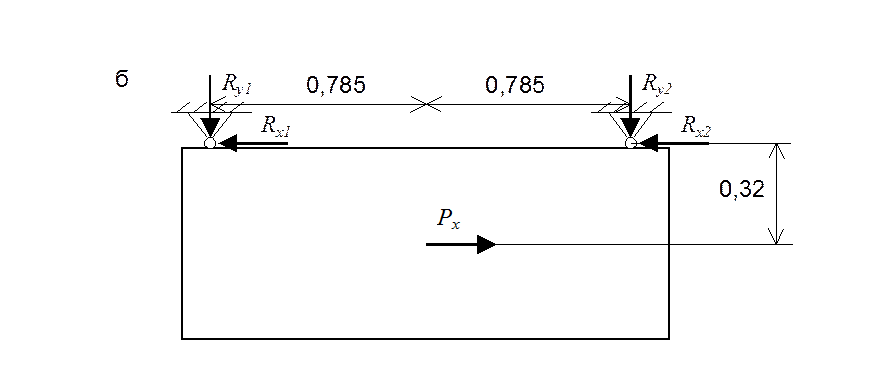
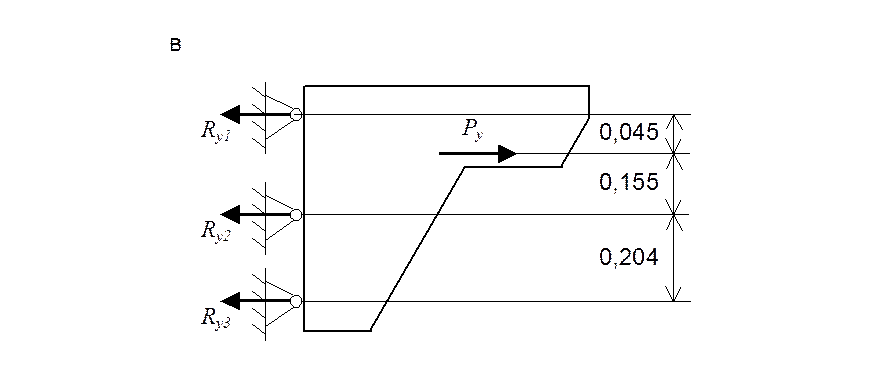
Рис. 2.3
3. Элементы крепления вентиляционного короба
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.