Лекция 9 проф. С.А. а
Содержание лекции 8. Указаны различия аналитических расчётов переходных процессов в моделях аналоговых и дискретных САУ. Естественно, приведены формулы предельного перехода, определяющие значение начальной и конечной РФ. Пояснена методика (процедура) расчета переходного процесса и сформулированы три полезных следствия. Изложена новая версия "скрытых" колебаний в ДСАУ. Кратко изложены соображения лектора об основных методах синтеза ДСАУ в плоскости " Z".
6.7. Синтез ДСАУ в плоскости " Z"(новая методика).
Авторы ( , ) назвали разработанный алгоритм методом "прямого программного синтеза" (ППС) линейных ДСАУ.
Основные характеристики и свойства метода ПС.
1. Метод в разработанной форме не пригоден для синтеза линейных аналоговых систем.
2. Метод предназначен для получения последовательных компенсационных регуляторов в полиномиальной форме при синтезе электромеханических систем (ЭМС) с дискретным управлением .
3. Настройки синтезированного регулятора выполняются при отработке детерминированного "единичного" сигнала.
4. Настройки синтезированного регулятора производятся во времени (а не в частотной области) и реализуются программно. Поэтому и метод назван "прямым программным".
5. Для метода ППС пригодны различные структуры линейных ДСАУ, для которых известны типовые эталонные переходные функции.
Суть метода состоит в нижеследующем. Пусть задана ПФ аналогового объекта ДСАУ в виде (1. 9)
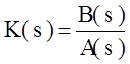 ,
(1. 9)
,
(1. 9)
где A(s) и B(s) известные полиномы модели объекта1).
Запишем ДПФ "не скорректированной" разомкнутой дискретной системы с экстраполятором Э0
![]() (2.9)
(2.9)
Обычно мы пользуемся записью ДПФ в виде отношения полиномов
![]() , (3. 9)
, (3. 9)
где
степень полинома "нулей" k ниже степени полинома
"полюсов" m, и в предельном случае ![]()
__________________________________________________________________
1)Обычно "объект" - это линейная модель неизменяемой силовой части ЭМС, включающей: усилитель мощности с блоком управления, электродвигатель с передаточным устройством, рабочая машина и необходимые датчики - преобразователи информации.
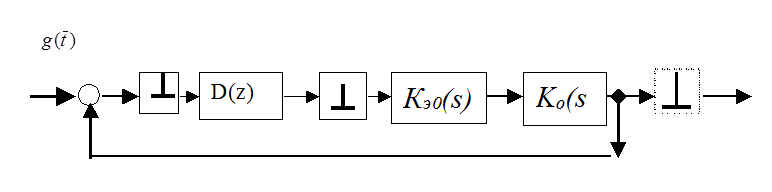 |
Рис 1. 9
Схема синтезируемой системы изображена на рис 1.9. Здесь реализована дискретная коррекция в полиномиальной форме с ДПФ вида
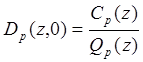
Тогда ДПФ скорректированной системы в разомкнутом виде будет:
![]() .
(4. 9)
.
(4. 9)
Здесь линейные полиномы ![]() полностью
известны.
полностью
известны.
Небольшое, но важное отступление -
пояснение.
При исследовании моделей ДСАУ часто бывает удобнее эти полиномы представлять
слагаемыми с отрицательными степенями аргумента "z". Тогда форма ДПФ
сохраняется, а полиномы записывают в виде ![]() и
т.д. При этом символ смещения "ε" сохраняют только при ДПФ, а при
полиномах, для упрощения записи, опускают. Выполним эту процедуру на конкретном
примере (2. 9).
и
т.д. При этом символ смещения "ε" сохраняют только при ДПФ, а при
полиномах, для упрощения записи, опускают. Выполним эту процедуру на конкретном
примере (2. 9).
![]() . (2. 9)1
. (2. 9)1
Поделив все слагаемые полиномов числителя и знаменателя (2. 9)1 на A0zm, получим:
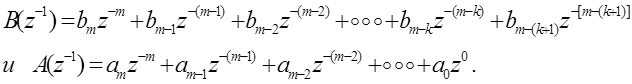 |
![]() . (2. 9)2
. (2. 9)2
Постарайтесь уяснить эту процедуру. Она использовалась и в лекции 8.
Необходимо найти ДПФ регулятора ![]() . Это можно сделать тремя
способами.
. Это можно сделать тремя
способами.
Первый способ. На основании деления известных полиномов (4.9)
получаем искомые полиномы числителя ![]() и
знаменателя
и
знаменателя ![]() модели регулятора. Деление
следует выполнить в форме (5. 9).
модели регулятора. Деление
следует выполнить в форме (5. 9).
![]() . (5.
9)
. (5.
9)
Тогда
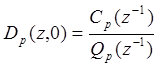 .
(6. 9)
.
(6. 9)
При этом следует иметь в виду, что значения отрицательных степеней полиномов регулятора в выражении (6. 9) может быть оказаться выше, чем степени полиномов числителей и знаменателей в (5. 9). Поэтому встает вопрос о разумном "усечении" степени полиномов регулятора. В этом проявляется специфическая особенность ДПФ полиномиальных регуляторов
Второй способ. На основании выражения(4. 9) получаем искомую ДПФ полиномиального регулятора в следующем виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.