Итак, в координатах q1 и q2 задаемся некоторым (пожалуй, предельно -допустимым) начальным значением параметра ПИД регулятора q0i. На отрицательной полуоси ординат q1 отмечаем два отрезка равные q0i и 2q0i.Через точки b и d проводим прямую, соответствующую уравнению q1= - (q2+q0i).
Слева в том же масштабе в координатных осях q1 и q0 проводим прямую О - В, соответствующую уравнению q0=-q1. На этом заканчиваются вспомогательные построения, связанные с использованием неравенств (20. 1. 9),(20. 2. 9). В результате получаются треугольники ОАВ и bcd, только внутри которых могут располагаться допустимые значения варьируемых параметров ДПФ регулятора q0, q1 q2.
Теперь задаемся значением q0 (точка 1), выбираемзначение q1 (точка 2) и находим q2 (точка 4). По формулам (20.3. 9) - (20. 5. 9) заканчивается процесс расчета параметров регулятора.
 |
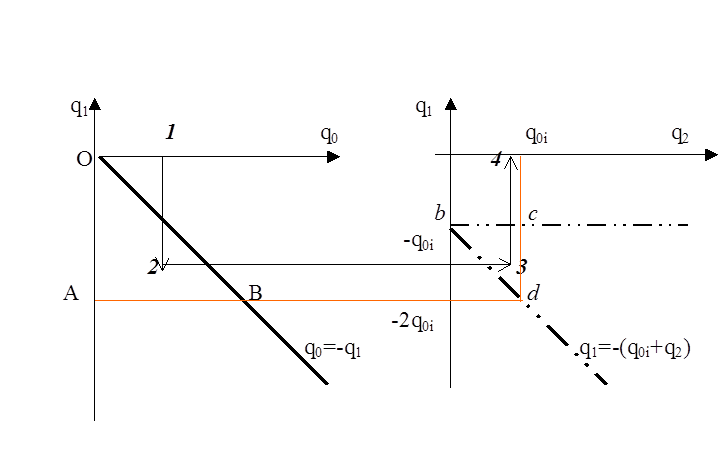Рис. 5.9.
Заключение Этот метод заимствован нами из литературы [29]. Были предложены и другие методы расчета параметров ДПФ регуляторов при больших интервалах квантования. Например, метод" весовых коэффициентов" (С. Ковчин) и метод " квадратичных оценок с использованием суммарных модифицированных наименьших квадратов" (K C. Rattan) (США). В обоих последних случаях авторы методов ставили целью получить такие настройки регуляторов ДСАУ, чтобы их динамические характеристики были близки к подобным характеристикам аналоговых систем
Скорректировано 17.01.08., вторая коррекция 04.04.08. третья коррекция 18.04.10
Четвертая коррекция 12.04.2011.
Приложение 9
К расчету желаемых характеристик для динамического синтеза ДСАУ
с л.а.х. вида 2 - 1 - 2 - 3 - 2 - 1 - 0
Эти материалы не относятся к содержания лекции 9, а необходимы для выполнения задач синтеза ДСАУ методом В.А. Бесекерского.
Задана передаточная функция (ПФ) модели аналогового объекта
(1)
Функция (1) разбивается на модель ПИ регулятора и модель объекта с экстраполятором нулевого порядка
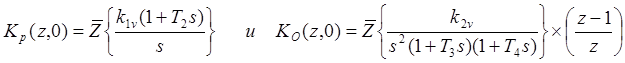(2)
Для вычисления K0 (z,0)выполним разложение дроби
(3)
Коэффициент k2v сохраним как общий сомножитель. Постоянные будут такими.
(4)
Введем соотношение
(5)
Из
формул (2) первый сомножитель (при интегрировании прямоугольниками) 
,
(6)
и второй сомножитель, где 
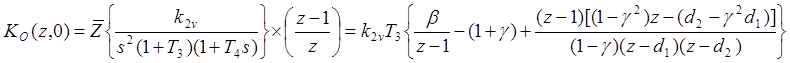.(7)
Полное произведение двух сомножителей дает ДПФ разомкнутой системы и дискретным ПИ регулятором и астатическим аналоговым объектом третьего порядка в таком виде.
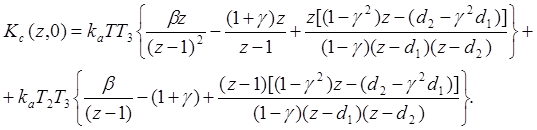(8)
Раскрытие сложного выражения (8) упростим следующим образом. Общий знаменатель имеет полином N(z),представленный в таком виде:
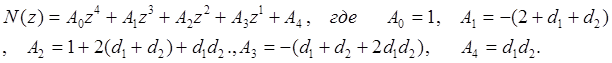
Полином числителя M(z) имеет шесть слагаемых, которые выпишем отдельно, преобразовав их общие множители. Для первых трех слагаемых множитель
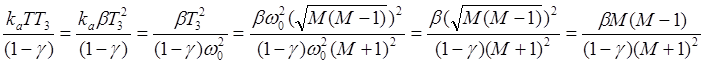. (9)
Аналогично
(9) для последних трех слагаемых общий множитель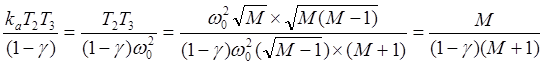 
(10)
Если обозначить выражение (10), как B1, тогда (9) приобретет такую форму:
(11)
В методе "динамического синтеза" для ДСАУ значения M, β, и γ задаются, поэтому B1 и B2 становятся в каждом случае постоянными числами. Приступим теперь к записи коэффициентов числителя
;
;
.
(12)
;
;
.
Преобразования Mi (z) достаточны, чтобы вычислить полином числителя ДПФ
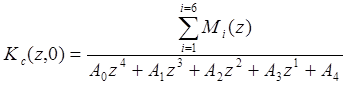(13)
Последний необходимый для "динамического синтеза" параметр - "добротность по ускорению" ka=ω02 также вычисляется в относительных единицах.
После несложных преобразований можно получить:
относительная угловая
скорость. (14)
Итак, при расчете таблиц показателей качества ДСАУ в
функции показателя колебательности "М" при каждом значении M=const
и β =const рассчитывается свое значение 
.
В этом состоит одно из различий синтеза ДСАУ от синтеза САУ.
Прилагаемые к тексту лекций таблицы рассчитаны при β=0,05; 0,1; 0.2; 0,5; 1,0 и 2,0. Значения М=1,05; 1,1; 1,2; 1,3; 1,5; 1,7; !,8; 1,9; 2.0; 2,2.
Скорректировано. 02. 04. 09. Повторно - . 18. 04. 09. И 18. 04. 10
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.