Различия аналитических расчётов переходных процессов в моделях аналоговых и дискретных САУ. Синтез ДСАУ в плоскости " Z"(новая методика), страница 7

При конструировании регуляторов для управления технологическими процессами, постоянные времени которых измеряются минутами и часами, задают большие интервалы квантования, чтобы проще технически реализовать регулятор, "сильно не растягивая" рекуррентные соотношения, подобные (14. 9)*, из - за малости периода квантования Т. Тогда нужно использовать иные способы выбора приемлемых параметров регуляторов.

Наконец, интегрирование можно выполнить по способу прямоугольников (в двух вариантах) или "методом трапеций" и иными способами "использования Z форм"²⁾.

Две группы таких вопросов попытаемся пояснить в этом разделе

6. 9. 2.Анализ алгоритмов и расчет параметрически - оптимизируемых компенсационных регуляторов при малых интервалах квантования

Пропорциональный интегрально- дифференциальный (ПИД) регулятор в САУ реализует необходимые показатели качества. За счет пропорциональной составляющей он подавляет внешние помехи и второстепенные возмущения, за счет интегральной составляющей увеличивает быстродействие системы и исключает её статическую ошибку, за счет дифференциальной составляющей повышает устойчивость САУ. Исходная схема регулятора изображена на рис.1.9.

Вначале запишем алгоритм аналогового прототипа регулятора

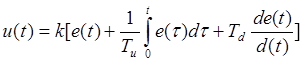.                                              (15. 9)

При малых интервалах квантования Т можно перейти без особой погрешности к следующему алгоритму:

.                                         (16.9)

Алгоритм (16.9) не рекуррентен, поскольку для вычисления суммы РФ

_________________________________________________________________

²⁾Не будем здесь касаться, и пояснять разные приемы и методы численного интегрирования. Это предмет других учебных курсов, которые вы изучали.

нужно много блоков (регистров) памяти. Так - как u[n,0] на каждом такте вычисляется заново, то ошибки вычислений не накапливаются. В этом, пожалуй, единственное достоинство алгоритма (16. 9). Найдем рекуррентный алгоритм, предварительно вычислив u[(n-1),0] по формуле (16. 9).

.

Вычитая полученное уравнение из предыдущего, после ряда простых преобразований получим:

,                                         (17. 9)

где .

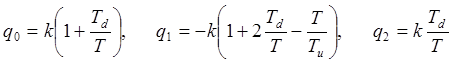Видно, что (17. 9) соответствует рекуррентному алгоритму вычисления u[n], так - как к сумме вычисленных в его правой части значений прибавляется только u[n-1].

Положим, что  оригиналы, изображения которых есть . Тогда из выражения (17. 9) по известным правилам (см. гл. 2, раздел 2. 4) получим ДПФ ПИД-регулятора в такой форме

.                                               (18. 9)

Несложно получить рекуррентный алгоритм программной реализации во временной области и схему аппаратной реализации регулятора по только что изложенным  описаниям.

6. 9. 3. Алгоритмы параметрически  - оптимизируемых компенсационных регуляторов при больших интервалах квантования

При больших интервалах Т не сохраняется соответствие между разностями РФ и производными непрерывных функций, суммами РФ и интегралами от непрерывных функций. Поэтому нельзя воспользоваться соответствиями между q_i и параметрами аналогового ПИД-регулятора, как в формуле (17. 9). Нужны другие условия для определения q_i  в выражении (18. 9), которое справедливо при любых интервалах квантования.

Пусть выход ПИД-регулятора имеет вид, изображенный на рис. 4.9.

Если принять:

Следовательно:

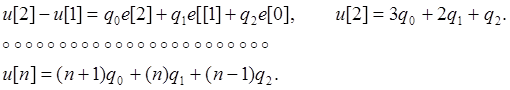                                (19. 9)

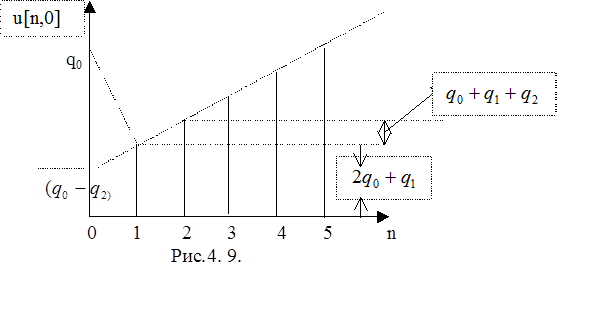При u[1]<u[0], как изображено на рис.4. 9, из условий (19. 9) можно получить следующие полезные неравенства:

q₀>2q₀+q₁, откуда q₁<-q₀, поскольку q₀>0;                               (20.1. 9)

               q₂>-(q₁+q₀), поэтому  q₂>0;                                                        (20.2. 9)

               k=(q₀-q₂) коэффициент передачи ПИД-регулятора;                (20.3. 9)

 относительная добротность по скорости регулятора;   (20.4. 9)

относ. постоянная дифференцирования регулятора            (20.5. 9).

Теперь ДПФ ПИД-регулятора запишем так:

                                                     (21.9)

Вычислить параметры регулятора при больших интервалах квантования можно по выражениям (20.1. 9) - (20. 5. 9), если воспользоваться вспомогательными графиками, построенными на рис.5.9.