Различия аналитических расчётов переходных процессов в моделях аналоговых и дискретных САУ. Синтез ДСАУ в плоскости " Z"(новая методика), страница 2

.                                                                           (7. 9)

Вопрос об "усечении" степени ДПФ регулятора упрощается. Специальные исследования доказали, что алгоритм решения задачи (7. 9) проще, чем (5.9) - (6. 9).

Третий способ. На основании того же выражения(4. 9) получаем искомую ДПФ регулятора в преобразованной форме следующего вида:

,                               (8. 9)

где  изображения "выхода" и "входа" модели скорректированной ДСАУ в "z" области.

 

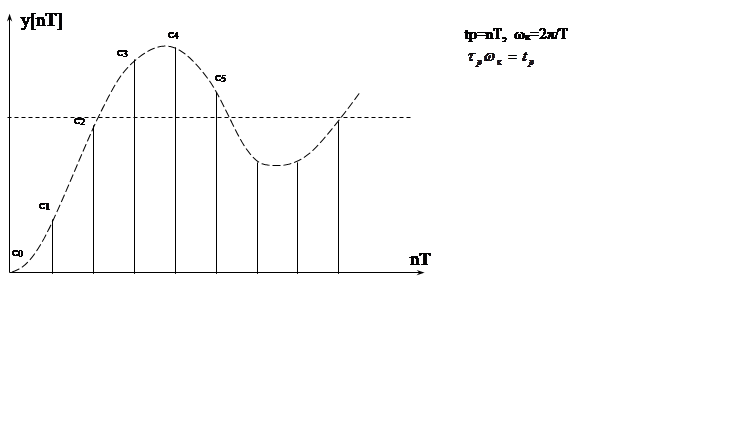
Рис. 2. 9.

Если принять  в форме  [см. формулу (3. 8), лк. 8] и вычислить её для различных типовых структур ДСАУ и g(t)=1(t), то . Тогда выражение (8. 9) приобретает такую форму:

                                                        (8. 9)¹

Форма (8. 9)¹ наиболее близко соответствует названию метода. В самом деле! в своих коэффициентах несет информацию о переходной функции скорректированной системы, а [1-] - аналогичную информацию об ошибке. Деление же полиномов есть ДПФ разомкнутой скорректированной ДСАУ.

Пусть будут вычислены семь первых значений (см. рис. 2. 9.) с₀     с₆..

Тогда произведение (1-z^-1)= можно раскрыть так:

                                (9. 9)

где  и .

Аналогично, выражение , будет равно:

                                    (10. 9)

где коэффициенты  имеют те же значения, что и в формуле (9.9).

После этих преобразований формула (8. 9)¹ может изображаться различно, а именно:

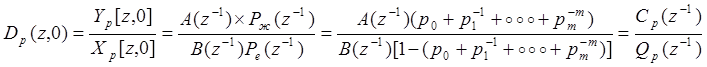,       (8. 9)¹¹

или

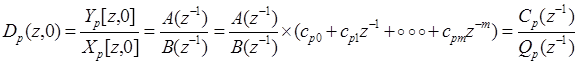.        (8.9)¹¹¹

Реализация синтеза предполагает выполнения следующих условий.

1. Форма (8.9)¹¹предпочтительнее для реализации регулятора, чем форма (8.9)¹¹¹,ввиду сложности вычисления  коэффициентов . Например, . с_р1=р₁,

с_р2=р²₁+р_2., но уже и дальнейшая сложность этих выражений возрастает.

2. Чтобы коррекция была физически реализуема, нужно иметь равный или меньший порядок полинома числителя C_p(z^-1)(m_р) от порядка полинома знаменателя Q_p(z^-1)(n_р)в этих выражениях, т.е.m _pn_p. В этом и состоит сущность "усечения" степени . Но обычно полином B(z) на один два порядка меньше A(z). Тогда на столько же увеличивают порядок полинома , беря дополнительные ординаты с₆, с₇ переходной функции (рис.2. 9), но, не меняя порядок полинома .

3. Пока не доказано какое количество интервалов "m" необходимо иметь для представления Y_ж(z^-1) в формуле (8.9)^!! и каково должно быть условие:.Мы использовали первые семь значений функции Y_ж(z^-1) при нулевых начальных условиях. Но можно ли  получить адекватное выражение для

D_p(z,0) при последующих значениях функции Y_ж(z^-1)  и ненулевых начальных условиях?

Покажем применение методики на конкретном примере.

Аналоговый объект управления имеет ПФ

Совместно с экстраполятором нулевого порядка, ДПФ объекта будет такой:

,                                    (11. 9)

где  - интервал квантования, k_v2  - добротность объекта по скорости

Теперь перепишем K₀(z)

,   (11.9^!

где:

Поделив слагаемые числителя и знаменателя  

на , получим:

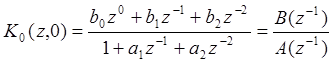,                                                            (11. 9)^!!

где .

Такими процедурами привели ДПФ объекта управления к необходимой для синтеза регулятора форме (11. 9)^!!

Дискретный пропорционально - интегральный регулятор имеет ДПФ:

.                                                                            (12. 9)

Прототипом ДСАУ является аналоговая система с желаемой л.а.х. 2 - 1 - 2. Поэтому постоянные времени Т₂ и Т₃ находятся в известном соотношении.

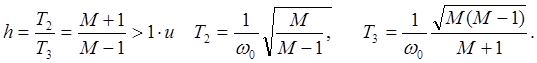
Перемножая выражения (11. 9) и (12. 9), в конечной форме получим:

,                                                          (13. 9)

где ,

,   добротность системы по ускорению.

Чтобы разрешить (6. 9), (7. 9) или варианты (8. 9), воспользуемся табл. 1.,которая позволяет выбрать ординаты Y_ж(z)

                                                                                                            Таблица1

Показатели качества цифровых автоматических систем