Различия аналитических расчётов переходных процессов в моделях аналоговых и дискретных САУ. Синтез ДСАУ в плоскости " Z"(новая методика), страница 6

Для систем с моделями 4 - го порядка соответствующие таблицы и формулы представлены в приложении 9 к материалам курса.

Для синтеза ДСАУ с экстраполяторами любого порядка и для моделей объектов без ограничений порядков пригодна методика синтеза по третьему способу реализации. Здесь важны знания о трех взаимосвязанных задачах (проблемах).

1. Задание при синтезе таких эталонных (желаемых) переходных функций h_ж(t), которые могут быть физически реализованы при заданных параметрах модели объекта.

2. Методика "усечения " порядка полиномиальных регуляторов.

3. Методика выбора оптимального значения величины интервала квантования Т и взаимосвязи его с величиной учитываемой наименьшей постоянной времени модели объекта τ_min ()? При большом  Т можно получить неустойчивую модель ДСАУ, а при малом Т нереализуемо "длинный" полином регулятора и переход к аналоговым моделям.

Поэтому в последующих лекциях будет изложен и другой метод синтеза ДСАУ.

6.8. Программная реализация корректирующих устройств

Метод z-преобразование позволяет получить очень простой и  удобный способ программной реализации корректирующих устройств, регуляторов и других технических устройств, математические модели которых представлены в z-преобразованной форме.

Пусть синтезированный нами в предыдущем параграфе регулятор по форме (8.9)¹¹ имеет такую ДПФ.

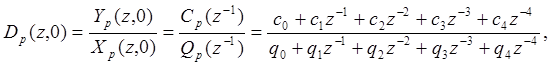                            (14. 9)

 - изображение РФ выхода корректирующего (программируемого) устройства,  -  то же для "входа" устройства.

Перепишем выражение (14. 9) в иной форме

При переходе во временную область принимаем: - несмещенная РФ - оригинал . Умножение  на z^-k , соответствует сдвигу аргумента в области оригинала на " - к" интервалов квантования (см. гл. 2, раздел 2. 4). Аналогичные правила относятся и к . Все коэффициенты с_i и q_i разделены (делятся) на q₀, приобретая "верхний индекс" - штрих с_i^! и q_i^!. Тогда выражение (14. 9)* примет форму алгоритма программной реализации вычислительного устройства во временной области (14. 9)

                           (14. 9)**

Этот алгоритм легко реализовать на любом промышленном контроллере (или ином вычислительном устройстве) и вычислить сумму времён всех элементарных операций умножений, сложений, (вычитаний) и переносов чисел из регистров в другой регистр, что и определит минимально необходимое время периода квантования Т в ДСАУ¹⁾. Упрощенная схема программируемого регулятора изображена на рис.3. 9

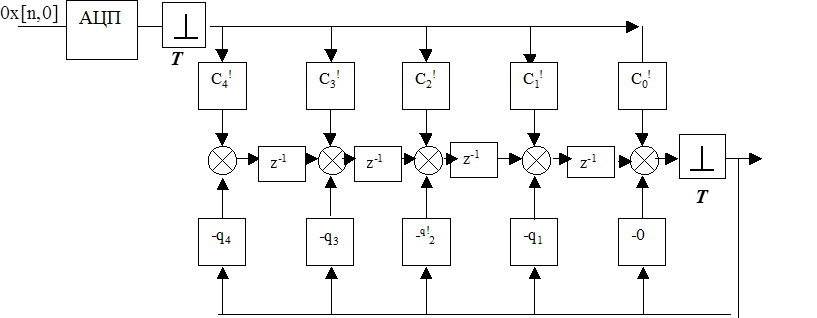Рис.3.9.

Итак, с помощью z-преобразований легко решаются задачи исследования устойчивости и анализа, линейных ДСАУ, а так же программные реализации во временной области различных алгоритмов управления. Задачи синтеза систем пока разработаны недостаточно. Третий способ синтеза (при программной реализации процедур) сулит существенные выгоды времени его выполнения.

__________________________________________________________

¹⁾ Примечание. Впрочем, задачу программной реализации алгоритмов управления уже решали в курсе, читаемом А. Н. Щербиной или А. Л .Логиновым при изучении промышленных контроллеров. Однако программная реализация ПИД-регуляторов подчас вызывает затруднения у студентов. Поэтому я (С. Ковчин) добавил следующий раздел, не прочитанный в 2006/07 уч. году. В 90 - е годы этому практически важному вопросу в системе знаний уделялось 2 - 3 лекции.

6.9. Особенности программной реализация пропорционально - интегрально - дифференциальных (ПИД) регуляторов.

6. 9. 1.Исходные положения

Обычно различают конструирование дискретных регуляторов при малых и больших интервалах квантования и различных способах интегрирования. Кроме того, напомним, что есть компенсационные регуляторы и регуляторы состояния. Последних регуляторов не будем касаться.

Для ЭМС (из - за малых постоянных времени объекта, измеряемых миллисекундами и  сотыми и десятыми долями секунды) можно использовать малые интервалы квантования и настройки дискретного регулятора выполнять по настройкам аналогового прототипа, если таковой имеется.