Суть двух критериев оценки устойчивости линейных ДСАУ и рекомендации по их использованию. Исследование переходных процессов ДСАУ в плоскости Z

Лекция 8 проф.

            Содержание лекции 7. Изложена суть двух критериев оценки устойчивости линейных ДСАУ и даны рекомендации по их использованию. Описан новый метод построения областей устойчивости в пространстве параметров системы.

ГЛАВА 6. Исследование переходных процессов ДСАУ в плоскости Z

6. 1. Исходные положения

Расчет переходных процессов в ДСАУ выполняется значительно проще, чем в аналоговых системах. Тем более ускоряются расчеты с применением современных вычислительных средств. Естественно, используются ДПФ замкнутых систем, записанные в обычной форме (1. 8).

, .                                                               (1. 8)

Далее представляются  изображения смещенных, или несмещенных, решётчатых функций в виде формул (2. 8)

 .                                                (2. 8)

Остается только напомнить, что любое из выражений (2. 8) (например первое)) нужно суметь записать  в полиномиальной форме (3. 8) со слагаемыми, расположенными по убывающим степеням "z".

.             (3. 8)

Тогда коэффициенты С₀….С_к … С_m будут оригиналами решётчатых функций y[0, ε]…y[k, ε]….y[m, ε]. Причем, вычисления по формуле (3. 8.) продолжаются не до , а до равенства ординат С_m= С_m+1= С_m+2 и т.д., если, конечно, на вход системы приложен постоянный сигнал g(t)=const.

Если для замкнутой ДСАУ представить (2.8) в следующей форме:

,                                                     (2.8¹)

а затем найти корни полиномов , то расчет переходных процессов можно выполнить по аналогу формул Оливера Хевисайда, которые используют при расчете непрерывных САУ [9]. Однако эти процедуры требуют выполнения существенно сложнее вычислительных операций и большего их количества, чем расчеты по формулам (2.8). Поэтому процедура (2.8¹) практически не используется.

6. 2. Формулы "предельного перехода" и их применение

Перед выполнением расчетов по формуле (3. 8) полезно проверить начальное и конечное значения решётчатых функций по формулам "предельного перехода". В плоскости они будут иметь такой вид:

 s, z=e^sT; 

 s,z^sT;                                               

Хотя эти формулы  аналогичны подобным выражениям для непрерывных систем

но получить верхние выражения непосредственной заменой в нижних формулах  и  на Y(z) нельзя Порядок получения "z" "предельных переходов" подробно описан в работе [9] и нами не приводится.

6.3.Построение переходного процесса ДСАУ в плоскости Z

Итак, мы продолжаем объяснять процедуру (методику) получение полиномиальной формы (3. 8) для Y(z, 0), записанной в виде (2. 8).

Сначала выполним следующие преобразования для Ф(z, 0):

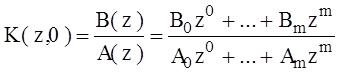. Исходная несмещённая ДПФ разомкнутой системы. Соответственно ДПФ замкнутой системы будет:

.                                            (4. 8)

Если все слагаемые полиномов B(z) и  A^!(z) поделить на A^!_mz^m, то получим выражение (5. 8) тождественно равное (4. 8).

 ,                                         (5. 8)

где b₀=0, поскольку переходный процесс начинается при с=0 (через теорему предельного перехода: z=exp(sT)→∞, и y[n, 0]=0)¹⁾.

___________________________________________________________________________

¹⁾Замечание Р. Горковенко. Вообще, по ходу дела кажется, что степень полинома числителя могла быть меньше. Тогда несколько первых коэффициентов b_i могли быть нулевыми.      Ответ С. . Хотя, Родион, Вы и правы, но степень полинома B(z)может существенно отличаться от степени исходного полинома B(s). Поэтому, какие еще коэффициенты b_i  равны нулю, выяснится по ходу выполнения описываемой процедуры. Но, если b₁,=0, то физически это будет означать, что переходный процесс в ДСАУ запаздывает относительно аналогичного процесса в непрерывной системе на интервал квантования Т .Это отставание, прежде всего, связано с экстраполяцией информации.

Но теперь полиномы числителя и знаменателя записаны слагаемыми с убывающими степенями "z". Символически это отражено записью .

Для получения Y(z, 0), в виде (2. 8) осталось задать G(z). Пусть . Тогда Y(z, 0), с учётом преобразования (5.8), получит такой вид:

.               (6. 8).

. Будьте внимательны! В последнем выражении коэффициенты в знаменателе уже другие, чем те, которые были прежде (фактически, я (Р.Г.) думаю: a₁=a'₁–1,  и т. д.)²⁾

_______________________________________________________________

²⁾Замечание Р. Горковенко.. По большому счету, мы уже получили  выражение (6. 8), которого добивались. Остается выяснить, что теперь с ним делать? Нам оно необходимо в другом виде, а именно в полиномиальной форме (3. 8). Почему? Потому что, как помним, -преобразование для решетчатой функции представляется в виде суммы последовательности значений этой функции, причем каждый последующий член делится на все более высокую степень аргумента z, то есть так:

А наше выражение выглядит как отношение двух многочленов. Чтобы получить его в нужном, только что описанном виде, раньше (40 - 50) лет назад был популярен способ деления числителя на знаменатель "в столбик" (или "уголком") – как этому (делению многочленов) учили в школе. В этом случае, поскольку многочлены, в общем случае, не будут делиться друг на друга нацело, будем все время получать остатки и продолжать деление до тех пор ,пока не получим равные и постоянные значения коэффициентов слагаемых .Это будет означать, что переходный процесс в модели ДСАУ закончился. В результате получать ряд: