Лекции10 проф.
Содержание лекции 9. Изложена методика синтеза ДСАУ в плоскости Z, разработанная на кафедре САУ СПбГПУ и указаны три способа её использования. Описана схема решения примера синтеза и приведены все необходимые вспомогательные материалы. Описан алгоритм решения задач программной реализации коррекций и других (линейных) вычислительных устройств с помощью Z преобразования. Ввиду особой практической важности отдельный раздел посвящен программной реализации дискретных ПИД-регуляторов.
ГЛАВА 7. Методы повышения качества обработки информации в ДСАУ
7.1. Исходные положения
В дискретных системах управления погрешности преобразования информации имеют две основные причины:
Первая причина связана с процедурами задержки передачи информации, обусловленными тем, что все операции сложения (вычитания) умножения (деления) и переноса – занимают определенное время и, в сумме, должны уложиться в интервал квантования. Преобразователи информации аналого-цифровые (АЦП) и цифро-аналоговые (ЦАП) также вносят свою "лепту" в эту задержку.
Например, если в ЦАП нет
физически реализованного таймера, то при времени обработки информации
"τ<T" в цифровом регуляторе приходится для аналогового объекта с
ПФ ![]() и экстраполятором Э0 вычислять
"приведенную" ДПФ в таком виде [27]:1)
и экстраполятором Э0 вычислять
"приведенную" ДПФ в таком виде [27]:1)
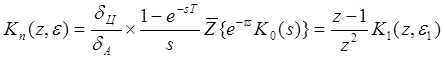 ,
(1. 10)
,
(1. 10)
где
![]() . Обычно
. Обычно ![]()
/_________________________________________________________________________________________________
1) Обращаю Ваше внимание на очень важное примечание к формуле (1. 10).Оно относится и ко многим другим формулам этого курса. Формула (1. 10) символизирует ПФ разомкнутой ДСАУ. В её тракт передачи сигнала управления последовательно входят АЦП и ЦАП (условно) как безинерционные усилители со своими передаточными коэффициентами кА =1/δА кЦ=δЦ /1. Таким образом, в ДПФ разомкнутых систем входит сомножитель:
![]() . Этот сомножитель мы видим
в первоначальной записи (1. 10). Но бессмысленно выбирать аналоговые кванты
(разрядность) преобразователей разными Младшие разряды не
будут работать. Поэтому, как правило, δА= δЦ и,
следовательно,
. Этот сомножитель мы видим
в первоначальной записи (1. 10). Но бессмысленно выбирать аналоговые кванты
(разрядность) преобразователей разными Младшие разряды не
будут работать. Поэтому, как правило, δА= δЦ и,
следовательно, ![]() . В последующей
записи формулы этот множитель (как и во многих других) упущен. Нужно
помнить и понимать, для каких воздействий и помех преобразователи будут
передавать информацию не последовательно, а независимо друг от друга???
. В последующей
записи формулы этот множитель (как и во многих других) упущен. Нужно
помнить и понимать, для каких воздействий и помех преобразователи будут
передавать информацию не последовательно, а независимо друг от друга???
Другой вариант математической модели ДСАУ может возникнуть, если её аналоговый объект имеет "чистое" запаздывание, которое намного больше длительности интервала квантования "τ>>T". Это обычно имеет место в моделях технологических процессов с большими постоянными времени.
Вторая причина связана с тем, что вместо операции дифференцирования используют разности РФ, а вместо операции интегрирования используют суммы РФ. Далее, при работе с решетчатыми функциями неизбежно используются экстраполяторы, которые вносят свои погрешности. Как было доказано во второй главе лекций, эти операции имеют малые расхождения только при длительности интервалов квантования стремящихся к нулю. Но тогда бессмысленно использовать дискретные математические модели технических устройств и применять более сложный математический аппарат дискретных функций.
Эту "Теорию дискретных систем управления" и нужно то использовать только тогда, когда дискретные алгоритмы управления принесут больше практической пользы, чем аналоговые структуры. По сути дела для распознавания уровня таких профессиональных задач и предназначен, в первую очередь, этот курс.
Естественно, говоря о погрешностях преобразования информации, как и в аналоговых системах, сохраняются требования к точности датчиков преобразователей, к малому дрейфу параметров аналогового объекта управления. Возрастает интерес к схемным решениям, уменьшающим погрешность отработки сигнала управления в статике и динамике, и к другим известным в науке мероприятиям.
Например, если в аналоговой системе первого порядка увеличить её постоянную времени Т0 на 10%, то независимо от величины Т0 время переходного процесса изменится тоже примерно на 10%. В ДСАУ того же порядка погрешность корней будет зависеть еще и от величины интервала квантования. Так, при Т0=1с, вариации +Δ Т0 =0,1с и Т=0,1с погрешность корня z0 от вариации Т0 будет примерно1 %, а при Т=1,0 с погрешность z0 будет около 10 %.
Поэтому чувствительность и точность ДСАУ, обусловленные иными свойствами, кроме двух указанных причин, не будем затрагивать в этой главе.
7. 2. Линейные экстраполяторы любого порядка
7. 2.1. Получение передаточной функции экстраполяторов любого порядка
(дополнительные сведения)
Ранее (см. гл.4) мы обсуждали вопрос о возможности использования экстраполяторов не только нулевого, но и первого порядка. Иногда возникает задача получения экстраполяции решётчатых функций и более высокого порядка. Для решения подобных задач целесообразно использовать вторую интерполяционную формулу Ньютона в таком виде:
![]() (2. 10)
(2. 10)
где ![]() и
и ![]() .
.
На основании выражения (2. 10) для
экстраполятора нулевого порядка, полагая что ![]()
![]()
![]() ,
получим:
,
получим:
![]()
![]()
В этом интегральном преобразовании было использовано: ![]()
Несмещённую дискретную передаточную функцию (ДПФ) экстраполятора нулевого порядка (Э0) с последовательно включенным аналоговым объектом [K0(s)] получим в таком виде:
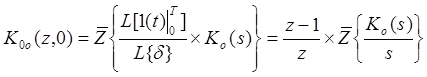 .
(3. 10)
.
(3. 10)
Аналогично, для смещённой ДПФ того же соединения будем иметь:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.