Модель экстраполятора первого порядка. Изучение свойств моделей линейных ИС. Данные расчета частотных характеристик экстраполятора первого порядка

Лекция 4. проф.

1.8. Модель экстраполятора первого порядка

Обсуждение содержания предыдущей лекции

Важно! 1. Итак, при дискретном преобразовании информации идеальным импульсным элементом (ИИЭ) спектры РФ, кроме основной четно-симметричной амплитудо - частотной  характеристики, (основной составляющей спектра) входного непрерывного сигнала приобретают бесконечное количество таких же боковых спектров. Нельзя сказать, чтобы это было "плохо" (это "чистая" математика), но это, по крайней мере, значительно осложняет изучение дискретных систем (Р. Г.) и искажает информацию в реальных ДСАУ (С.К.)

2. Мы выяснили, что для получения "хорошего" спектра необходимо установить идеальный фильтр на выходе ИИЭ. Из - за невозможности его реализации, было предложено рассмотреть свойства нескольких видов реальных фильтров. В качестве простейшего фильтра предложен экстраполятор 0-го порядка (Э₀) и приведены его характеристики.

3.Цифровые автоматические системы (ЦАС) с квантованием входной информации по уровню и времени по физической структуре своих элементов (АЦП и ЦАП) являются нелинейными ДСАУ. Линеаризируя характеристики АЦП и ЦАП "методом секущих", сводим матем. модели ЦАС к линейным импульсным системам (ИС). Следовательно, основным предметом этого курса является изучение свойств моделей линейных ИС.

Рассмотрим теперь принцип построения и действия экстраполятора 1-го порядка (Э₁), оговорившись, впрочем, что физически его реализовать сложно.

Э

Рис. 1.4, a

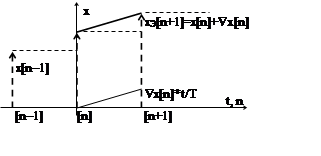Рис. 1.4, б

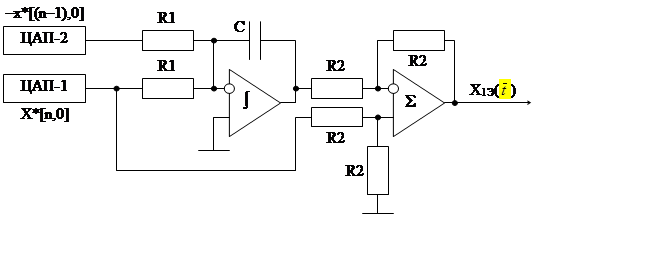
На рис 1.4,а представлена упрощенная электронная схема такого устройства. Принцип её работы состоит в следующем. В момент времени [nT] на вход 1ЦАП, который исполняет роль первого "регистра памяти", поступает цифровой сигнал, преобразуемый в аналогx^*[nT]^*) .Этим же сигналом прежнее содержание 1ЦАП x[(n-1)T] "перебрасывается "поразрядно во второй "регистра памяти" (2ЦАП) и с обратным знаком, в виде аналогового сигнала (минус) x^*[(n-1)T] поступает на второй вход интегратора. Следовательно, на выходе  интегратора формируется линейно - нарастающий сигнал  (см. рис 1.4, б) . Далее этот сигнал инвертируется по знаку масштабирующем усилителем. Сумматор () выдает аналоговый сигнал экстраполятора первого порядка (с обратным знаком)в таком виде:

.                                                               (1.4)

Поэтому в течении "n" интервала сохраняется постоянное значение сигнала , а в конце этого интервала (см. рис.1.4, б.) сигнал на выходе экстраполятора приобретает значение.

По истечении "n" - го интервала времени Т срабатывает таймер, управляющий работойвсейсхемы, замыкается электронный ключ К (рис 1.4, а.). Происходит "сброс в нуль" интегратора, цифровой сигнал x[(n+1)T,0] поступает на вход 1ЦАП. Далее, весь процес повторяется циклически, но уже на (n+1) интервале. Однако здесь не указаны: схема таймера, схема электронного ключа К и схема инвертора сигнала . Поэтому реальная схема такого экстраполятора ещё сложнее.

Передаточная функция экстраполятора 1-го порядка имеет такой вид:

.                                                                  (2.4.)^**)

Его амплитудо - и фазочастотные характеристики были получены в таком виде:

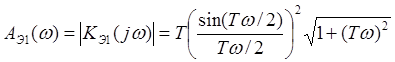
      (3.4.)

Появление множителя T в выражении для АЧХ  связано с преобразованиями выражения (2.4.) и размерностью входного сигнала экстраполятора любого порядка! В данных, нижеприведенной таблицы, коэффициент Т не учитывается.

___________________________________________________________

               ^*)Здесь, и всегда далее, символом * будем отмечать аналоговый сигнал, полученный из  РФ. Например, x*[kT, 0] аналоговый сигнал постоянной величины "x" на интервале времени kT< t <(k+1)T. Другой пример: Δ^*x[m, 0] линейно нарастающий сигнал постоянной величины равной РФ первой прямой разности сигнала "x" на интервале  при 0≤ t ≤T. Более компактно (возможно, и понятнее) предыдущее предложение можно записать так: Δ^*x[m, 0] = x[(m+1), 0] - x[m, 0]=A=const.; Δ^*x[m, 0] =A×, при 0≤ t ≤T.Постарайтесь запомнить смысл символа *при любых РФ.

^**) Строгое доказательство достоверности (2.4.) есть в работе ([9] с. 86).

.

Данные расчета частотных характеристик экстраполятора первого порядка