Модель экстраполятора первого порядка. Изучение свойств моделей линейных ИС. Данные расчета частотных характеристик экстраполятора первого порядка, страница 2

ω/ωK	0	0.25	0.5	0.75	1	1.5	2	2.5	3
A(ω)	1	1.51	1.34	0.434	0	0.427	0	0.256	0
Аиф(ω)   φ(ω)	0	–0.82π	–π	–1.93π	–2π	–3π	–4π	–5π	–6π

                                                Рис. 2.4.

График модуля АЧХ экстраполятора Э₁ построен на рис. 2.4. Сопоставляя данные экстраполяторов Э₀ и Э₁ можно сделаь такие выводы.

1. Экстраполятор Э₁, как фильтр, не обеспечивает значительных преимуществ по сравнению с экстраполятором Э₀, а в области частот ω/ω_K >1 имеет примерно в два раза бóльшую погрешность (см. рис. 7.3 и рис. 1.4).

2. В сфере действия идеального фильтра 0< ω/ω_K<0,5 Э₁ по модулю имеет лучшие характеристики , чем Э₀ (см. рис. 7.3 и рис. 1.4).

3. Фазовый  сдвиг (АФХ) у Э₁ вдвое больше, чем у Э₀ (см. табличные значения  ФЧХ

4. Аппаратная реализация экстраполятора Э₁ очень сложна (см. рис.1.4.) и требует значительных добавок в интерфейс любого вычислительного устройства.

5. Поэтому, прежде чем строить такой фильтр физически очень важно обосновать необходимость именно его применения.

В- дальнейших лекциях будут приведены примеры целесообразного применения экстраполяторов первого и более высоких порядков и оригинальная программа их реализации, без добавления интерфейса.

1.8. О неправомерности использования теоремы Котельникова - Шеннона для выбора частоты квантования в ДСАУ

Формулировка обсуждаемой теоремы¹⁾. Любую непрерывную функцию с любой (по формулировке В. Котельникова) точностью можно представить в виде ряда:

,                                                                  (4.4.)^*

где .Причём, модуль спектра  равен нулю при ω_с^**).

Естественно предположить , как  дискретный аналог четно-симметричной функции времени f(t) с нереальным условием **⁾для информации (сигналов), отрабатываемой ДСАУ (См. примечние 1 лк.3).

Теперь исследуем второй сомножитель ряда

.                                                                                 (5.4.)

Примем, для простоты доказательств, условие теоремы ω_С =0,5ω_К. Случай ω_К/2 > ω_С, требует более сложных доказательств того же результата.

Обозначим:Теперь можно записать:

.                                                                       (6.4)

Подставляя (6.4.) в числитель и знаменатель формулы (5.4.)получим следующее выражение:

.

Следовательно, сомножитель (5.4) прибрел такую форму:

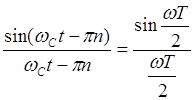                                                                             (7.4.)

Итак, исследовав формулу ряда Котельникова (4.4.), приходим к выводу, что второй сомножитель под знаком суммы представляет собою характеристику экстраполятора 0-го порядка (без множителя Т).

_____________________________________________________________

¹⁾Примечание 1. Эта теорема была неоднократно предложена разными исследователями, в связи, с чем имеет несколько "фамильных" наименований. В частности, в 1933г её предложил в виде (4. 4.) советский инженер (и впоследствии академик АН СССР) В. А. Котельников, в 1948г известный американский ученый в области теории управления и информатики Клод Шеннон ("импульсная теорема" - " теорема отсчетов"его имени). Задолго до них, в 1915 году английский математик Уиттекер (1873 - 1956 г.г.)  (Wittaker E.T University of Edinburg) сформулировал подобное утверждение.