Модель экстраполятора первого порядка. Изучение свойств моделей линейных ИС. Данные расчета частотных характеристик экстраполятора первого порядка, страница 3

Все "основоположники" теории дискретных систем управления в (50 - 60) - е годы XX века считали необходимым сослаться на эту теорему, как на фактор, подтверждающий целесообразность получения спектра дискретного сигнала вида рис 3. 3. Поэтому у инженеров - практиков уже в течение полувека бытует ложное мнение о легкости выбора частоты квантования ω_К (или Т_к) из условия: ω_К > ω_С. Впервые существенно усомнился в этом (по мнению автора лекций) В. Гусев[13]. Мы уже обсудили ошибочность такого мнения (см. лк.3.) Так что же такое ряд (4. 4.)? Выше изложено личное мнение об этом автора(С. К.)

^*)  Это была одна из пяти (пятая) теорем, изложенных В. А. Котельниковым в работе" О пропускной способности эфира и проволоки в электросвязи". Подробнее см. [3].

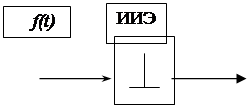
Следовательно "ряд Котельникова  - Шеннона" (4.4.) представляет собою математическую модель непрерывной функции времени, квантованную идеальным импульсным элементом  и восстановленную экстраполятором Э₀. (См. рис.3.4.). Какой либо другой полезной информации по сравнения с фундаментальной формулой (11.1) выражение (4. 4) не несет. Таким образом, указанная теорема реально не дает каких - либо оснований для выбора частоты квантования в ДСАУ.

 

 

Э0

                                   f [nT]                       f* [nT]

 

Т

Рис.3.4.

ГЛАВА 2. Дискретные преобразования

2.1. Введение

Дискретные функции часто удобнее подвергнуть преобразованию с тем, чтобы расчеты и моделирование проводить в области изображений, а не в области временных функций.

Для линейных непрерывных систем достаточно владеть одним только преобразованием Лапласа, однако для исследования моделей дискретных систем и решения разностных уравнений следует иметь представление о 3-х преобразованиях и уметь пользоваться хотя бы двумя из них.

2.2. Дискретное преобразование Лапласа

Отметим сначала, что этот термин введен, безусловно, не самим Лапласом (чьи труды относятся к началу 19 века), а учеными более поздних времен при разработке дискретных систем в середине 20 века. Это: Цыпкин Я.и др. (СССР)[3], Баркер Р. Х., Гуревич В.,Шеннон К. и др. (США).

Определение.

.                                              (8.4.)

Сравним (8.4) с формулой непрерывного преобразования Лапласа: .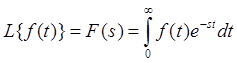

Здесь аргумент q является безразмерной величиной (точнее, имеет размерность угла в радианах). Отсюда появляется еще одно замечание. Рассмотрим q в виде комплексного числа в алгебраической форме: . Очевидно, σ, и  имеют также размерность радиан. К решетчатой функции f[n,0] предъявляются такие же требования, как и к f(t). Она должна быть ограниченного роста, "слева "от нуля тождественно равна нулю.

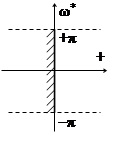
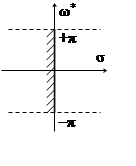          Поскольку угол изменяется с периодом 2π, то нас будет интересовать не только "основная полоса" плоскости q, отвечающая значениям Im(q)=  в пределах от–π - 0 до +π и все боковые полосы, от+π до +3π и т.д., а также от –π до –3π и т. д.т. Точнее, все "левые" полу σ полосы простирающиеся от мнимой оси. Обратим внимание на штриховку слева, – она обозначает область, в которой должны располагаться корни устойчивой системы. Причем весь комплект                       Рис.4.4.