Модель экстраполятора первого порядка. Изучение свойств моделей линейных ИС. Данные расчета частотных характеристик экстраполятора первого порядка, страница 5

1). Свойство линейности. Оно может быть сформулировано так: изображение линейной комбинации РФ равно такой же комбинации их изображений.

{αf₁[n]+βf₂[n]}=αF₁(z)+βF₂(z),                                                       (12.4.)

где F₁(z) ={f₁[n]} и F₂(z)={f₂[n]}.

2) Теорема запаздывания и упреждения. Сдвигу  аргумента оригинала (РФ) вправо (запаздыванию) на "k" целых тактов соответствует умножение в области изображений на z^-k. Аналогичному сдвигу аргумента РФ влево (упреждению) соответствует умножение в области изображений на z^+k. При нулевых начальных условиях эти свойств запишем в таком виде³⁾:

запаздывание {f[n-k]}=z ^-kF(z),                                                       (13. 4)

упреждение   {f[n+k]}=z ^+kF(z),                                                     (14. 4)

где {f[n]}=F(z) изображение РФ.

3) Изображение  разностей. Для прямых разностей, при нулевых начальных условиях, имеем:

 {Δ^kf[n]}=(z–1)^kF(z).                                                                        (15..4.)

При тех же условиях для обратных разностей получим:

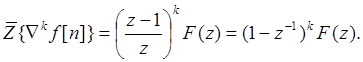                                                (16.4.)

При ненулевых начальных условиях эти преобразования существенно сложнее. Например,.       (15.4¹.)

Таким образом, алгебра разностных уравнений легко подвергается  - преобразованиям.

Иногда приходится пользоваться обратными "зет" преобразованиями ^-1. Они выполняются по формуле

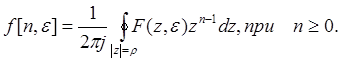
Интеграл берется по окружности с центром в начале координат плоскости "z" и с радиусом , где z_v  особые точки (корни) модели F(z,ε).

2.5. Дискретное  - преобразование

Невозможность использования частотных методов при  преобразовании привела к тому, что в 1955 году американские исследователи

_______________________________________________________________

³⁾ Примечание 3. При ненулевых начальных условиях выражения (13.4) и (14.4.) существенно усложняются (так же как и L{f(t)}), а именно:

запаздывание{f[n-k]}=z^-k[F(z)+,                                               (13.4¹)

упреждение{f[n+k]}=z^+k[F(z)-,                                                (14.4¹)

где f[-r] и f[r] решетчатые функции в указанных суммах не равные нулю.

Джонсон и Линдорф (Johnson G. W., Lindorf D.P.) воспользовались идеей немецкого математика Мёбиуса (1790 - 1868 г.г.) и предложили применить конформное преобразование его имени в таком виде:

z=(1+Tw/2)/(1–Tw/2)                                                                         (17.4.)

Тогда можно ввести - преобразование и для решетчатых функций f[n]:

{f[n, ε]}=F(w, ε) или {f[n, 0]}=F(w, 0).                                         (18.4)

Поскольку с помощью вычетов легко найти  преобразование РФ, то выражения (18.4) обычно разрешают так:

{f[n, ε]}=F(w, ε)=F(z, ε)                                                        (19.4.)

Преобразуя формулу (17.4.), достаточно просто получить⁴⁾

w=jλ=2/T*tg(ωT/2)                                                                          (20.4.)

Здесь λ -  псевдо-частота, а окружность единичного радиуса z-плоскости (или вся мнимая ось плоскости "q") переходят целиком в мнимую ось w-плоскости. В самом деле, при ω = 0, λ=0, при ω = +, λ, а при ω= -, λ.

______________________________________________________________

⁴⁾Примечание 4. Выражение (20.4..) найдем, записав иначе (17.4.).

что и требовалось получить.

Скорректировано .