Методика синтеза ДСАУ в плоскости Z, разработанная на кафедре САУ СПбГПУ и три способа её использования, страница 5

                                                                  (12. 10)¹

где , и i=0, 1,2, 3, 4, 5, …..и т.д. При этом γ_i

должна вычисляться на каждом интервале.

                                                           (12. 10)¹¹

где  условия для определения ε_i здесь такие же, как и в (12. 10)¹.

Выписав все расчетные соотношения, алгоритм вычисления динамического процесса в этой нелинейной дискретной систем, пояснять не будем. Поскольку этот вопрос выходит за рамки курса линейных дискретных систем³⁾.

Первые работы по исследованию ДСАУ с ТК мы начали с Чжань Ан Нянем в1986г., а в 88 г. получили патент на это устройство. Затем многократно возвращались к этой теме. Имеются исследования частотных характеристик ТЭ и других экстраполяторов, устойчивости ДСАУ с Т.Э, сравнительных характеристик ДСАУ с различными экстраполяторами. Аспирант И. Макулов предложил треугольный экстраполятор с вертикальным передним фронтом. Его ДПФ  будет

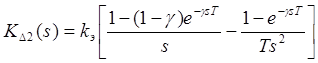. Смысл коэффициента к_э тот же, что и в экстраполяторе с АШИМ. Работы по исследованию ДСАУ с нелинейными экстраполяторами далеки от завершения. Эта проблема оказалась очень сложной.

Большие разработки проведены по ДСАУ с однополярной и двухполярной ШИМ. Но все это класс нелинейных ДСАУ.

Итак, мы имеем набор различных линейных и нелинейных экстраполяторов. Свойства двух из них мы уже сравнили. Результаты более широкого исследования представлены в таблице. Здесь показаны модели различных аналоговых объектов и их параметры. Приведены предельные значения добротностей по скорости моделей импульсных систем с такими объектами и с различными экстраполяторам. Указаны параметры переходных процессов .

_____________________________________________________________-____

³⁾ Замечу только что эту задачу аналитически нельзя решить по методике, предложенной в работе [5]. Она была решена у нас в1998 - 99г.г. в диссертации магистра Т.Лопатьневой и Самером С. Эль Нсеиром в кандидатской диссертации и вовсе не в связи с исследованием "треугольных" экстраполяторов. Просто предложенный нами алгоритм аналитического исследования динамики моделей нелинейных дискретных систем позволяет решать по единой схеме разнообразные задачи. (С.К.)

.                                                                                                     Таблица

Примечания:

1. Порядок линейных экстраполяторов: "0 пор." - нулевого порядка; "1 пор.." - (аппаратно - реализуемый) экстраполятор первого порядка."1 экв." -  эквивалентный (программно - реализуемый) экстраполятор первого порядка. Нелинейные экстраполяторы: треугольный и АШИМ  -экстраполятор с"амплитудно и широтно-импульсной модуляцией".