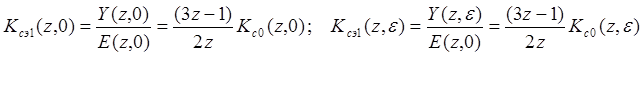Методика синтеза ДСАУ в плоскости Z, разработанная на кафедре САУ СПбГПУ и три способа её использования, страница 3

,     (7. 10)

где  выражения для не смещенной и смещенной ДПФ разомкнутой системы при наличии эквивалентного экстраполятора первого порядка.

В формуле (7. 10) принято:

выражения для не смещенной и смещенной ДПФ разомкнутой системы, включающей последовательное соединение экстраполятора нулевого порядка и аналогового объекта.

3. Фактическая реализация "эквивалентного" экстраполятора изображена на Рис. 2.10. как последовательная программа выполнения алгоритма (6. 10) в блоке регулятора D(z) с выдачей результата на существующий в ДСАУ ЦАП, который и исполняет роль экстраполятора нулевого порядка. Таким образом, каких - либо реальных схемных переключений блоков или портов не требуется.

4.Сопоставляя свойства известного экстраполятора первого порядка (4. 10) и "эквивалентного " (6. 10) видно, что первый реализуется аппаратно интеграторами в аналоговой части системы. По двум параллельным цепям сумма однократно интегрируемой и двукратно интегрируемой информации поступает на вход аналогового объекта с математической моделью K₀(s). В реальной ЭМС эта информация поступает на вход усилителя мощности. В предыдущей главе мы "уже ломали голову" как получить рекуррентный алгоритм обработки информации интегратора в ПИД-регуляторе? Теперь еще получили двух кратно - интегрируемую "прелесть"!!?? Меня "увольте" от решения этой задачи. Я давно сделал выбор в пользу "эквивалентных" экстраполяторов повышенных порядков. А вы, мои уважаемые слушатели, поразмышляйте над результатами следующего аналитического эксперимента. Ваших знаний вполне достаточно, чтобы сделать свои выводы.

Пример. Задана модель аналоговой разомкнутой САУ в таком виде.

Предельные значения относительной добротности по скорости (граница устойчивости) для аналоговой САУ, определенное по критерию Гурвица (k_vT)_пр.=0,600; для ДСАУ с экстраполятором первого порядка,  -  по критерию Джури (k_vT)_пр.=0,580; для ДСАУ с "эквивалентным" экстраполятором первого порядка, определенное  так же по критерию Джури(k_vT)_пр.=0,586

Рис 1.10.

            Переходные процессы моделей замкнутых систем рассчитывались при k_vT=0,5 (k_vT)_пр. для аналоговой системы по формуле Хевисайда, а для ДСАУ по типовой программе Джури.

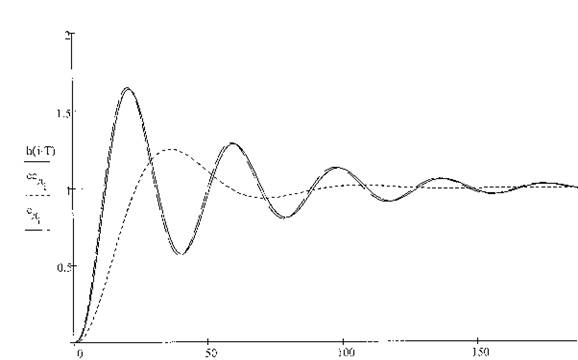На рис.1. 10 по оси абсцисс время отложено в миллисекундах (интервалах квантования). Ординаты точек с индексом "с_Дi" соответствуют процессу в модели ДСАУ с экстраполятором нулевого порядка, они близки к ординатам аналоговой САУ, а точки с индексом "сс_Дi" соответствуют процессу в модели ДСАУ с эквивалентным экстраполятором первого порядка. В последнем случае качества динамического процесса неизмеримо лучше (в конкретной достоверности таких результатов я сомневаюсь [С. К.).Почему это могло произойти? Просто ли так, я (С. К.) назвал Джань Ан Няня талантливым ученым?

7.3 2. Эквивалентный экстраполятор 2-го порядка

(дополнительные сведения)

Итак, мы продолжаем рассматривать различные экстраполяторы с целью определить плюсы и минусы применения разных их видов на практике, а также обсуждаем возможность их реализации (программной).

Слушатель Р.Горковенко Минуточку! А что такое эквивалентный экстраполятор 2-го порядка? Как мы видели, ЭЭ первого порядка в качестве выходного сигнала дает линейный, отвечающий среднему значению выходного сигнала на выходе обычного экстраполятора 1-го порядка на интервале от n до n+1, то есть постоянный сигнал уровня x_Э1(t)=1.5*x[n]–0.5*x[n–1] для t от nT до (n+1)T, если не ошибаюсь. Верно ли аналогичное для ЭЭ 2-го порядка? И по формуле и по записям, вроде, именно так, но я бы еще и картинку нарисовал для красоты и лучшего восприятия...

С.Ковчин. Все верно, Родион! Только картинку ожидал, что Вы нарисуете по своей инициативе, а полезна она, несомненно.

Итак, формула для сигнала на выходе экстраполятора:

 

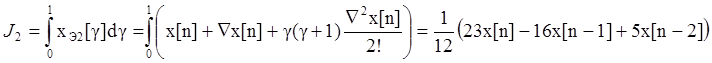
Получим z изображение для системы с таким экстраполятором:

                      (8. 10)

Здесь K_CЭ2 – ДПФ разомкнутой системы с эквивалентным экстраполятором второго порядка, а  – ДПФ той же системы, но с экстраполятором нулевого порядка. Как реализовать подобную систему? По-видимому,  так же как  с эквивалентным экстраполятором первого порядка, т.е. достаточно просто (см. рис.2. 10)

                                    Рис. 2. 10