7.4.Амплитудно-широтно-импульсный модулятор (АШИМ)
 Идею такого экстраполятора
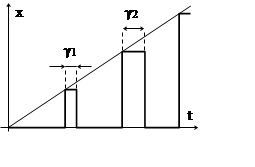
продемонстрируем на простом примере. Пусть имеется обрабатываемый сигнал вида x(t)=kx,
то есть линейно нарастающий. В начале каждого периода фиксируется величина входного
сигнала, и импульс на выходе экстраполятора Рис.3. 10.
Идею такого экстраполятора
продемонстрируем на простом примере. Пусть имеется обрабатываемый сигнал вида x(t)=kx,
то есть линейно нарастающий. В начале каждого периода фиксируется величина входного
сигнала, и импульс на выходе экстраполятора Рис.3. 10.
формируется с уровнем,
пропорциональным этой величине, также и длительность импульса
пропорциональна ![]() .
.
Здесь кэ коэффициент крутизны (передачи) экстраполятора нулевого порядка при АИМ. В этом случае обычно считают кэ=1. Соответственно расчет переходного процесса, например, по алгоритму Джури, намного сложнее.2). ________________________________________________________________
2)Методики расчета динамики в нелинейных ДСАУ, хотя и сложны, но много проще, чем в нелинейных непрерывных системах. Например, этим вопросам посвящены работы [5, 7, 10, 21, 31 и др.]. В нашей научной школе тоже есть ряд интересных работ этого направления. Но в этом учебном курсе мы стараемся избегать освещения нелинейных ДСАУ. Однако свойства нелинейных экстраполяторов часто оказываются эффективнее, чем линейных. В курсах для магистров ряд вопросов теории НДСАУ изучается.
. Р.Горковенко. Только длительность периода, я так понимаю, остается постоянной, раз это широтно-импульсный модулятор?)Таким образом, справедливы формулы=f1(x)=k1x – амплитуда выходного сигнала; γ=f2(x)=k2x – длительность импульса выходного сигнала.
Такой экстраполятор (рис. 3. 10) является нелинейным. Можно записать, что KАШИМ(s)=кЭ(1–e–γsT)/s, – но величина γ в этом выражении является переменной.
Далее познакомимся с еще одним экзотическим экстраполятором, который, как мы увидим, тем не менее, имеет крайне серьезные права на более широкое применение
7. 5. Нелинейный треугольный экстраполятор
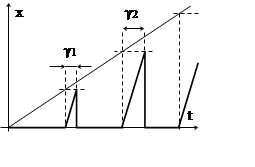 Этот экстраполятор похож на АШИМ тем,
что амплитуда и ширина импульсов пропорциональны зафиксированной в начале
периода величине входного сигнала. Отличие состоит в том, что сами импульсы
имеют не прямоугольную, а треугольную форму с Рис.4. 10.
Этот экстраполятор похож на АШИМ тем,
что амплитуда и ширина импульсов пропорциональны зафиксированной в начале
периода величине входного сигнала. Отличие состоит в том, что сами импульсы
имеют не прямоугольную, а треугольную форму с Рис.4. 10.
линейным нарастанием уровня до заданного значения и последующим мгновенным спадом до нуля.
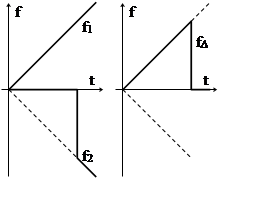 Скорость нарастания, то есть угловой
коэффициент "пологой" стороны треугольника одинакова для всех
импульсов и равна некоему заранее определенному максимально возможному уровню
входного сигнала, деленному на период, который также остается постоянным. То есть
kΔ=tgα=UMAX/T. Можно построить такие
"треугольные" экстраполяторы (ТЭ) и с вертикальным передним фронтом
импульса.
Скорость нарастания, то есть угловой
коэффициент "пологой" стороны треугольника одинакова для всех
импульсов и равна некоему заранее определенному максимально возможному уровню
входного сигнала, деленному на период, который также остается постоянным. То есть
kΔ=tgα=UMAX/T. Можно построить такие
"треугольные" экстраполяторы (ТЭ) и с вертикальным передним фронтом
импульса.
Как реализовать такой экстраполятор на современных электронных компонентах не будем рассматривать. Но как получить его математическую модель?
Будем рассматривать каждый треугольный импульс как разность двух линейных функций f1(t) и f2(t).
fΔ(t)=f1(t)–f2(t)=kΔt×1(t)–kΔt×1(t–τ), Рис. 5.10.
где τ=UВХ/kΔ – длительность импульса.
Передаточную Функцию ТЭ получим обычным образом,
Рис.6. 10
![]() . Поэтому определим L{f Δ(t)}.
. Поэтому определим L{f Δ(t)}.
![]()
Вычислим раздельно.
![]() (9. 10)
(9. 10)
В равенстве (9. 10) значение интеграла ![]() в тех же пределах, но
противоположно по знаку. Поэтому определение
в тех же пределах, но
противоположно по знаку. Поэтому определение![]() можно
упростить, ограничившись вычислением только
можно
упростить, ограничившись вычислением только ![]()
![]()
![]() .
.
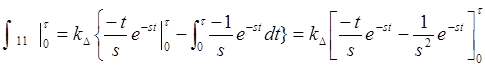 (10.
10)
(10.
10)
Если учесть, что γТ=τ, то преобразование (10. 10) даст такой результат:
![]() (11. 10)
(11. 10)
Итак, модель аналоговой части расчетной
нелинейной импульсной системы (рис. 6. 10) в этом случае
состоит из идеального импульсного элемента, блока "треугольного"
экстраполятора с ПФ (11. 10) и объекта с функцией KO(s),
соединенных последовательно. В свою очередь ТЭ состоит из двух параллельных
каналов передачи информации, в одном из которых включено нелинейное статическое
звено, блок "чистого запаздывания" и интегратор. В другом канале
включено линейное статическое звено с коэффициентом передачи ![]() , нелинейный экстраполятор
нулевого порядка и интегратор. Дискретная передаточная функция разомкнутой
нелинейной структуры, изображенной на рис 6. 10, подвергается
, нелинейный экстраполятор
нулевого порядка и интегратор. Дискретная передаточная функция разомкнутой
нелинейной структуры, изображенной на рис 6. 10, подвергается ![]() преобразованию по аналогии
со схемой "типовой ИС с Э0 при
преобразованию по аналогии
со схемой "типовой ИС с Э0 при ![]() (См.гл.4.)
(См.гл.4.)
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.