2. Обозначения символов и параметров kv - добротность САУ по скорости, T - интервал квантования в ДСАУ,
(kvT)пр. -предельное значение параметров, при котором замкнутая непрерывная САУ или ДСАУ выходят на границу устойчивости.
Параметры переходного процесса замкнутой системы при "единичном" входном сигнале: σ% - перерегулирование, tnn=nT - время переходного процесса при радиусе "трубки" Δ=2,0 %.
Можно, к большому удивлению, наблюдать, что наилучшей по динамике оказывается система с нелинейным треугольным экстраполятором. Личное мнение проф. Ковчина, что такой экстраполятор привносит в систему те же качества, какие получаются от добавления дифференцирующего звена, – а такая модификация системы в принципе улучшает устойчивость.
В целом улучшения возможны вплоть до того, что дискретные системы с треугольным интерполятором оказываются лучше, нежели непрерывные.
До некоторых пор существовала серьезная проблема с реализацией таких систем на практике – в связи с отсутствием генераторов линейно нарастающих сигналов большой мощности (действительно, треугольные импульсы тока (момента) выглядят красиво на бумаге, – но организовать их в электродвигателе, мощностью хотя бы 5 кВт – это сложная техническая задача). Впрочем, в последние десятилетия в области силовой электроники, это уже не такое непреодолимое препятствие. Есть и другие схемные решения такой задачи в реальных ЭМС.
Резюме. Если не затрагивать нелинейные экстраполяторы, которые программно реализовать сложно, то для повышения устойчивости и качества динамических режимов ДСАУ целесообразно применять экстраполяторы не нулевого порядка, а реализуемые программно эквивалентные экстрапляторы первого порядка
7.6. Повышения качества обработки информации в ДСАУ
модификацией ПИД-регуляторов
7. 6. 1. Исходные положения
В дискретных, а иногда и в аналоговых системах, применяя различные модификации ПИД-регуляторов, можно получить существенные изменения динамики их динамических процессов. Грамотному инженеру полезно знать эти приемы.
7. 6. 2. Алгоритм управления с заданным начальным значением сигнала выхода регулятора
Часто полезно ограничить сигнал на входе усилителя мощности в ЭМС. Тогда можно записать такое выражение для ДПФ замкнутой системы
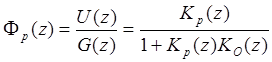
Используя принятые выражения для ДПФ объекта и регулятора второго порядка при b0=0 (см. раздел 6.9), запишем уравнение, разрешенное относительно U(z).
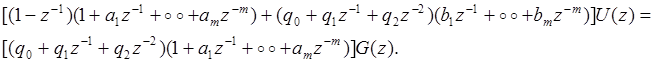(13. 10)
Выражение (13. 10) запишем во временной области в виде разностного уравнения при g[n]=1[n], ограничиваясь несколькими первыми членами:
(14. 10)
Из (14. 10) при n=0 имеем:
(14. 10)*
(14. 10)**
Подставляя из (14. 10)*u[0] в (14. 10)** и прибавляя u[0] как u[n-1] в
(14. 10)**, получим:
(14. 10)***
Только при g[0]=1[0] ,будем иметь:
Чтобы сделать u[1]<u[0] необходимо выполнить неравенство:
(14. 10)****
Итак, подставляя в выражение (14. 1)*
желательное значение 
, получим искомую
величину 
. Затем из неравенства (14.
10)****вычислим 
.
7. 6. 3. Алгоритм управления с ограничением влияния помех
в сигнале задания
Вместо обычного алгоритма (17. 9) для ПИД - регулятора выберем такую модификацию
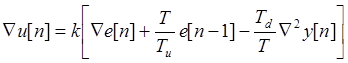(15. 10)
Здесь в дифференциальной составляющей исключено влияние задающего сигнала g[n] и присутствующих в нем помех. Кроме того, разность первого порядка заменена разностью второго порядка от выходного сигнала объекта, который всегда исполняет роль фильтра для высокочастотных сигналов.
По тому же принципу проделаем модификацию регулятора и по пропорциональной составляющей. А именно:
.
Поскольку
, то вышеуказанное
равенство станет таким
Теперь алгоритм (15. 10) будет.
.
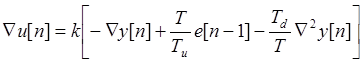(16. 10)
Влияние помех в сигнале g[n] сохранилось при интегрировании, но там оно существенно меньше. Этим не исчерпываются все варианты модификации ПИД - регулятора. Можно изменить метод интегрирования от "прямоугольников" на "трапеции", варьировать постоянную дифференцирования по различным критериям
Скорректировано 25.01. 08. , 05.04. 09. Скорректировано 17.04. 11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.