Машиностроение \ Теория дискретных систем управления

Суть двух критериев оценки устойчивости линейных ДСАУ и рекомендации по их использованию. Исследование переходных процессов ДСАУ в плоскости Z, страница 2

Сравнивая это выражение с предыдущим, мы можем заметить, что они идентичны.

Э. Джури предложил определять коэффициенты с_i из системы уравнений, получаемых с помощью ряда Лорана (учитывая ,что а₀=1):

b₀=c₀a₀.

Здесь 1 слагаемое, отсюда вычисляем c₀=0.

b₁=c₁a₀+c₀a₁.

Здесь 2 слагаемых, но одно "нулевое", находим с₁.

b₂=c₂a₀+c₁a₁+c₀a₂ .

Здесь 3 слагаемых, но одно "нулевое", находим с₂

("...и так продолжается бой…".)

b_m=c_ma₀+c_m–1a₁+...+c₀a_m.

Здесь, фактически, m слагаемых, вычисляем c_m. (7. 8)

(Коэффициенты b_i кончаются, значит дальше, слева, идут нули.)

0=[b_m+1]=c_m+1a₀+c_ma₁+...+c₀a_m+1.

Здесь m+1 слагаемых, вычисляем c_m+1.(Теперь и коэффициенты a_i кончились, – больше прироста слагаемых нет.)

0=[b_m+2]=c_m+2a₀+c_m+1a₁+...+c₀a_m+2.

Здесь то же(m+1) слагаемых, так как a_m+2=0, вычисляем c_m+2;

0=[b_m+3]=c_m+3a₀+c_m+2a₁+...+c₀a_m+3.

Аналогично, - (m+1) слагаемых, поскольку a_m+3=0, вычисляем c_m+3;

(...и так, до полного удовлетворения!...)

Примечание 3.С.Ковчин считает ,что по алгоритму Джури (7. 8) удобно вычислять и строить графики с помощью Exsel или Mathcad. Попытка решить ту же задачу прямым набором модели ДСАУ в Matlab и воспроизведение переходного процесса в этой аналитической модели ДСАУ дало иные результаты. Они воспроизведены в нижеследующем примере.

Пример. Задана схема ДСАУ, изображенная на рис.1. 8. с экстраполятором нулевого порядка. Передаточные функции (ПФ) элементов и параметры системы таковы:

Рис.1. 8.

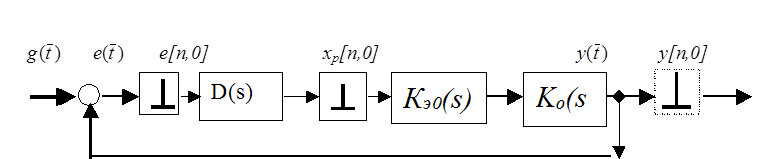ПФ регулятора ПФ объекта

Параметры системы: Т₁=10 мс , Т₂=2 мс , Т₃=4 мс, Т=1 мс - интервал квантования ИИЭ.

Относительная добротность объекта по скорости

ДПФ объекта с экстраполятором после преобразований и промежуточных вычислений была получена в таком виде:

ДПФ регулятора ,(совместно с блоком преобразования информации, который не изображен на рис.1. 8. и сущность которого здесь не может быть пояснена подробнее) имеет следующую структуру:

. (*)

Полное выражение (2. 8.), при единичном сигнале на входе, было получено в такой форме:

(* *)

Результаты расчета переходной функции ДСАУ, выполненные по формулам (7. 8.), (алгоритм Джури) на основе выражения (*) представлены в нижеуказанной таблице. Там же приведены результаты моделирования ДСАУ в Matlab.

Таблица

Джури	n	0	1	2	3	4	5	6	7	8	9
	y[n,0]	0,00	0,239	0,76	1,29	1,66	1,72	1,51	1,14	0,789	0,564
Matlab	n	0	1	2	3	4	5	6	7	8	9
	y[n,0]	0,00	0,24	0,78	1,32	1,66	1,78	1,543	1,211	0,8	0,612
Джури	n	10	11	12	13	14	15	16	17	18	19
	y[n,0]	0,544	0,69	0,939	1,17	1,3	1,29	1,18	1,01	0.858	0,783
Matlab	n	10	11	12	13	14	15	16	17	18	19
	y[n,0]	0,5	0,69	1,01	1,212	1,317	1,32	1,21	1,08	0,878	0,79
Джури	n	20	21	22	23	24	25	26	27	28	29
	y[n,0]	0.799	0,881	0,99	1,09	1,13	1,12	1.05	0,997	0,919	0,896
Matlab	n	20	21	22	23	24	25	26	27	28	29
	y[n,0]	0,81	0,91	1,0	1,1	1,13	1,14	1,1	1,0	0,9	0,896
Джури	n	30	31	32	33	34	35	36	37	38	39	40
	y[n,0]	0,909	0,946	1,0	1,04	1,05	1,04	1,01	0,98	0,954	1/0	1,0
Matlab	n	30	31	32	33	34	35	36	37	38	39	40
	y[n,0]	0,9	0,951	1,0	1,07	1,05		1,1	1,0	0,8	0,9	0,85

1 2 3 4 5

Скачать файл