Проф. Ковчин и его ученик Фан Лидзинь (Fayg Lijin) на моделях показали, что здесь "n" должно быть не любым целым, а нечетным, иначе поворот фазы создаст не положительную, а отрицательную обратную связь, гасящую "раскачивания" системы.
6.6. Краткий обзор методов синтеза ДСАУ в плоскости Z
Существует несколько таких методов синтеза , которые
очень пропагандируются в последние два - три десятилетия. Они основаны на
решение этой задачи во временной области. Оперируя дифференциальными или
разностными уравнениями, записанными в матричной форме (13. 8) для переменных
(координат) системы в нормальной форме Коши, находят вектор состояния
динамической системы в моменты времени it, начиная с t0.
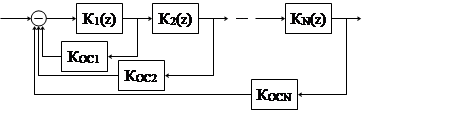
Рис. 3. 8.
В математической форме сказанное записывается так:
dx/dt=Ax+Bu, y=Cx+Du, (13. 8)
где x, u и y вектора переменных состояния системы, соответственно, размерностью: n×1, q×1, и m×1. A, B, C, и D матрицыпостоянныхкоэффициентов размерностью: n×n, n×q, m×n и m×q.
Далее, по всем переменным системы xi вводят обратные связи, изменяя передаточные которых Косi добиваются нужного поведения системы. Тем самым получают регулятор состояния (РС). Часто метод такого синтеза называют "методом пространства состояний" (МПС).
Однако на практике отнюдь не по любой переменной можно завести обратную связь – иногда это сложно физически (например, потребуется очень специфичный датчик) – иногда же нельзя даже принципиально. Кроме того, датчики непременно будут влиять на динамику системы, – все они в какой-то мере инерционны. Замыкая внутренние контуры через такую инерционную обратную связь [например, Koc1(s) -рис.3.8], мы повышаем степень "нулей" в выражении передаточной функции системы. Это может повлиять на её устойчивость.
Итак, МПС рекомендует иметь числитель ПФ нулевого порядка. Кроме того, для МПС требуется иметь фундаментальную матрицу, а это, по сути, означает, что необходимо знать полином знаменателя скорректированной замкнутой системы, которая обладает заданными показателями качества. Такая задача решается для аналоговых систем. Существует литература, например [56], где приведено около 400 таких полиномов от 2 до 8 порядка с указанными показателями качества скорректированной системы.
При использовании МПС для синтеза ДСАУ возникают новые нерешенные проблемы. Корнями полинома знаменателя ДПФ - N (z, 0) являются числа zi=exp(siT). Следовательно, в отличие от применения этого метода для непрерывных систем, (где работают с набором корней {si}) мы отягощены тем, что zi зависят еще и от периода квантования T, который, значит, нужно выбрать "наперед". И это только первая проблема.
Далее, если для непрерывных САУ разработаны взаимосвязи между параметрами полиномов N(s) и показателями качества синтезированной системы (о чем мы только что говорили) то для ДСАУ таких разработок нет. Это вторая проблема.
Таков, примерно, круг проблем, связанных с применением известных методов для синтеза ДСАУ. Поэтому в ЛПИ (СПбГПУ) много лет занимались решением задач синтеза ДСАУ, которые были доведены до разной степени практического (инженерного) использования. С одним из методов, разработанных мною, совместно с (выпускниками кафедры САУ) инж. В. Шендеровским (1989 - 1990 г.г.) и доц. (канд. техн. наук) (Dph)-Бернардом (Мубайедом Фадльем) Муафаком (Ливан) (1990 - 1994 г. г.) познакомимся на следующей лекции. И в чем его суть? На этом закончим большой раздел курса о применении Z преобразования в теории ДСАУ.
Скорректировано 15.12.07. Скорректировано повторно 30.03.09.и 06. 04.11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.