Различные схемы включения датчиков в главной обратной связи в ДСАУ. Методы исследования устойчивости линейных ДСАУ в плоскости Z

Лекция 7 проф.

Содержание лекции 6. Приведены различные схемы включения датчиков в главной обратной связи в ДСАУ. Указаны ДПФ систем с датчиком "мгновенного съема данных" и с датчиком "средних значений сигнала". Сделана попытка оценить влияние инерционности датчиков в аналоговых и дискретных САУ. Приведены ДПФ разомкнутых систем с различными экстраполяторами нулевого порядка.

ГЛАВА 5. Методы исследования устойчивости линейных ДСАУ в плоскости Z

5. 1. Критерий устойчивости Шур-Кона¹⁾ (примерно 1947 - 48 г.г.)

Необходимо записать полином знаменателя замкнутой системы в виде:

,                                                    (1. 7.)

а затем составить определитель Шур-Кона D_Ш-Ки проверить два условия.

1. Ни один минор не должен быть равен нулю , а это значит, что ни один корень не должен быть равен "единице"

2. Число перемен знаков в определителе , должно быть равно n, тогда все n-корней полинома N=0 будут лежать внутри окружности единичного радиуса на z- плоскости, следовательно, система будет устойчива.

Определитель  имеет 2n столбцов и 2n строк, , комплексно сопряженные значения коэффициентов в (1. 7.).²⁾

____________________________________________________________________

Я (С.Ковчин), могу только предполагать, когда появился критерий, и как возникло его название. Пожалуй, впервые его ввел в теорию дискретных систем управления Э. Джури [1], сославшись на работу Мардена (Marden. M), изданную Американским Математическим Обществом в 1949г. Только из этого первоисточника можно установить личности и математика Шура (известно два крупных немецких  ученых математиков с такой фамилией) и личность неизвестного в России Кона.

В случае комплексно - сопряженных значений коэффициентов полинома (1. 7)записывается дважды:

 и .

Следствие. Если обозначить , то все - четные должны быть больше нуля, а все  - нечетные должны быть меньше нуля.

Итак, из D_Ш-К можно составить:

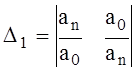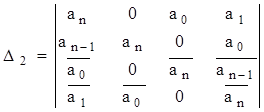,  ,   и т. д., а затем проверить соблюдение условий следствия, вычислив все "n"миноров.

Процедура использования критерия оказалась сложной, использование вычислительной техники помогает мало. Видимо, критерий применяли, для оценки устойчивости моделей дискретных систем управления технологическими процессами, математические модели которых имеют малый порядок и очень большие значения постоянных времени (минуты и десятки минут).

В электромеханических системах (ЭМС), порядки выше, а постоянные времени существенно меньше (часто, единицы и десятки миллисекунд). Поэтому, при вычислении миноров, их значения стремительно приближаются к нулю. Распознать положительность или отрицательность этих величин, с учетом накапливающихся ошибок вычислений, становится трудно.

 Мы не рекомендуем применять этот критерий устойчивости ДСАУ. Кроме того, критерий  не позволяет выявить "скрытые колебания " в ДСАУ.

5. 2. Критерий устойчивости Джури (1955 г.)

Теперь запишем полином знаменателя модели замкнутой дискретной системы в иной форме:

 при .                          (2. 7.)

Обратим внимание на то, что полиномы знаменателей в рассматриваемых критериях записываются различно.

Далее, автор критерия предлагает три варианта использования равенства (2. 7.) для решения задачи устойчивости дискретной системы.

Первый вариант он назвал детерминантной формой, второй вариант табличной формой, а третий - алгебраической формой. Автору лекций более простой представляется табличная форма. Он (С. Ковчин) также считает, что в этой форме заложена информация, которая позволяет не только оценить устойчивость ДСАУ, но и решить другие задачи. Это будет показано ниже. Итак, на основе выражения (2.7.) составим таблицу Джури.