Различные схемы включения датчиков в главной обратной связи в ДСАУ. Методы исследования устойчивости линейных ДСАУ в плоскости Z, страница 2

Из элементов таблицы Джури составим и вычислим следующие миноры:

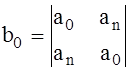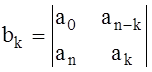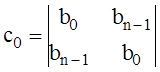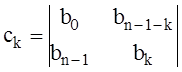, , ,     .      (3. 7.)

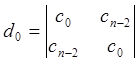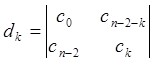, и т.д.

Суть критерия. Чтобы все корни полинома (2. 7.) находились внутри окружности единичного радиуса (т.е. модель ДСАУ была устойчива) необходимо  и достаточно соблюдение нижеуказанных неравенств.

1) .

2) , если n-четное, или , если n-нечетное.

3) ,

,                                                                            (4. 7.)

,

5. 3. Построение областей возможных вариаций параметров ДСАУ по  условиям критерия устойчивости Джури

Еще Э.Джури [1] обратил внимание на то, что условий (4. 5.) оказывается больше, чем необходимо для оценки устойчивости исследуемой системы. Но это обстоятельство не вызвало у него каких - либо конструктивных идей²⁾. Мы попытались использовать эти свойства, создав методику построения "гиперповерхностей и гиперобъёмов устойчивости" линейных ДСАУ в координатах варьируемых параметров³⁾.

Поясним содержание методики на конкретном примере. На рис. 1.7. представлена структура исследуемой системы .Она имеет объект с ПФ  и экстраполятор нулевого порядка  с ПФ . Объект имеет типовую структуру с л.а. х. 2 - 1 - 2

                                                           (6. 7.)

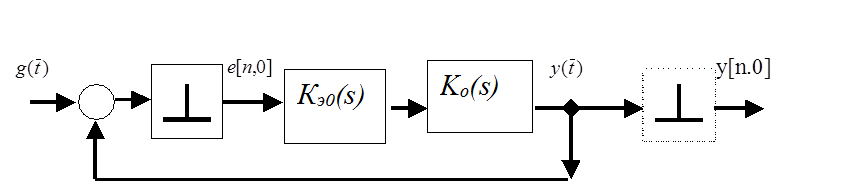Рис 1.7.

Аналоговая САУ устойчива при любых значениях добротности по ускорению к_а и при Т₂>T₃. Но в ДСАУ дополнительно влияет на устойчивость структура экстраполятора (фазовый сдвиг и соответствующее запаздывание)

отраженная соотношением: .

Поэтому, вначале найдем ДПФ разомкнутой системы  в таком виде:

            (*)

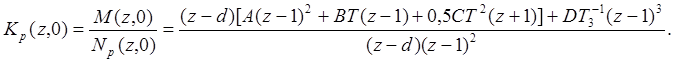В выражении (*) имеются следующие постоянные величины:

                        (**)

Если задать М=const, то по формулам (**) вычисляются все значения постоянных и функция N(z,0) - формула (2. 7.) ,будет разрешима относительно своих коэффициентов. Например, далее решение задачи выполняется при М=1,5, т.е. Т₂ = 5Т₃ по формуле (***) с заполнением табл. Джури и оценкой пределов четырех неравенств (4. 7.)

                                    (***)

 

^{_______________________________________________________________________________________________________}

               ²⁾  Метод D - разбиений разработан в СССР Ю. И.Неймарком (1947 г.) и, по сути дела, был неизвестен в 50 - е годы в США.

³⁾ Существенное участие в разработки методики приняли инж. А. В Дудко (вып. 2003 г) и магистр Т. Э. Ахмадеев (вып. 2006 г.).

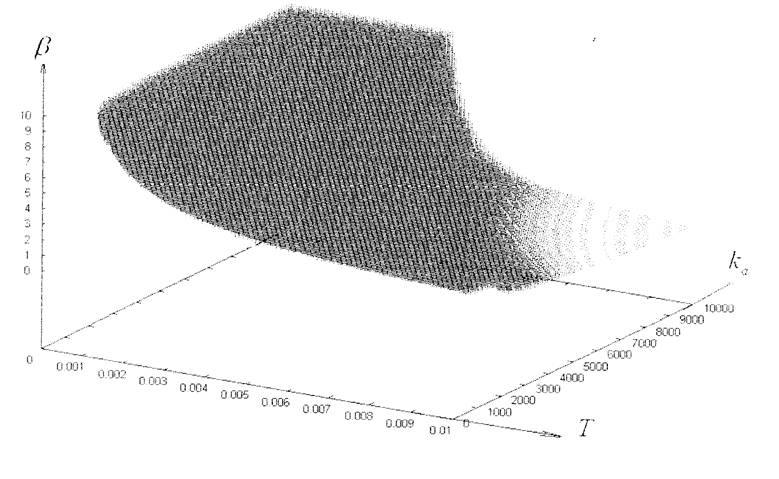
В этих неравенствах параметры варьировались в следующих пределах: 0,1мс <T<10мc - реальный диапазон изменений интервала квантования в ЭМС с цифровым управлением.

При β<<0,1 можно уверенно принять  и степень исследуемой системы понизить на один порядок, а при β >10, модель САУ должна рассматриваться только как аналоговая.

Добротность по ускорению ЭМС, как правило, меньше .

Систему неравенств можно успешно решать при заданных диапазонах варьирования параметров, написав программу на языке СИ. Далее полученные данные обрабатывались программным комплексом GNUPlot, результатом работы которого является гиперповерхность, изображенная на рис. 2.7. Повторяя расчеты при других значениях показателя колебательности М, получим объемную фигуру пределов  варьирования параметров. Нетрудно представить, что при увеличении М фигура будет сужать свой объем.

Таким образом, мы продемонстрировали новую методику оценки границ варьирования трех и более параметров линейной дискретно - аналоговой системы, обеспечивающих выделение областей её устойчивости. Напомним, что метод D разбиений, применимый только для аналоговых систем, допускает вариации только двух параметров. Понятно, что применимость методики эффективна только с использованием современных вычислительных средств.

Рис.2.7.

10. 12 07. Скорректировано и исправлено 04. 04. 09.