Нявызначаны інтэграл. Азначэнне і ўласцівасці нявызначанага інтэграла. Азначэнне нявызначанага інтэграла

Раздзел 4.Нявызначаны інтэграл.

§4.1.Азначэнне і ўласцівасці нявызначанага інтэграла.

Асноўнаю задачай дыферэнцыяльнага злічэння ёсць знаходжанне вытворнай дадзенай функцыі. Пры разгледжанні многіх пытанняў як матэматыкі, так і яе дасдасаванняў узнікае адваротная задача: для дадзенай функцыі  знайсці такую функцыю , каб . Аднаўленне функцыі па зададзенай яе вытворнай ёсць асноўная задача інтэгральнага злічэння.

1° Азначэнне нявызначанага інтэграла.

def. Дыферэнцавальная на інтэрвале Х функцыя  называецца першаіснаю для  функцыі  на Х, калі .

Тэарэма 1 (пра агульны выглыд першаіснай). Няхай функцыя  ёсць першаісная для  на Х. Функцыя  ёсць таксама першаісная для , калі і толькі калі .    

□ 1)(Неабходнасць). Няхай  ёсць першаісная для , г. зн.  і , або . Згодна з тэарэмаю пра супаданыя вытворныя .

2)(Дастатковасць). Няхай . Паколькі , то

 , г. зн.  – першаісная для . ■

Такім чынам, для дадзенай функцыі  яе першаісная  вызначаецца неадназначна, менавіта з дакладнасцю да сталага складніка. Для таго каб з сям’і першаісных вылучыць пэўную першаісную , дастаткова задаць пункт , які належыць графіку функцыі .  

def. Калі  ёсць першаісная для  на інтэрвале Х , то сукупнасць  першаісных для  называюць нявызначаным інтэгралам ад функцыі на Х  і абазначаюць

.                                               (1)

У гэтым абазначэнні знак называецца знакам інтэграла, – падінтэгральнай функцыяй, а – падінтэгральным выразам.  Аперацыю знаходжання нявызначанага інтэграла ад дадзенай функцыі называюць інтэграваннем. Яна ёсць адваротная да аперацыі. дыферэнцавання. 

Падінтэгральны выраз можна запісваць некалькімі спосабамі

.                                             (2)

2° Уласцівасці нявызначанага інтэграла.

1º.

□  ■

2º.

□  ■

3º.

□ Паколькі , то . З друго-га боку . Правыя часткі апошніх дзвюх роўнасцяў супадаюць, калі . Паколькі , то па зададзеным ліку  можна знайсці лік  і, наадварот, па зададзеным ліку  можна знайсці лік . ■

4º. .

□  Калі  , то  

.   ■

З уласцівасцяў 3º. і 4º. вынікае, што аперацыя інтэгравання мае ўласцівасць лінейнасці:

.

На падставе табліцы вытворных атрымаем табліцу нявызначаных інтэгралаў:

§4.2. Асноўныя метады інтэгравання.

1º. Метад падстановы.

У многіх выпадках увядзенне новай зменнай інтэгравання дае магчымасць звесці вылічэнне дадзенага інтэграла да табліцавага. Такі метад інтэгравання называецца метадам падстановы або метадам замены зменнай і выкарыстанне яго грунтуецца на наступнай тэарэме.

Тэарэма 1. Калі функцыя  мае першаісную  на прамежку Т, а функцыя  ёсць дыферэнцавальная на Х, прычым , то    

                                (1)

□ Дастаткова паказаць, што  ёсць першаісная для падінтэгральнай функцыі. Паводле правіла дыферэнцавання складанай функцыі маем

.           ■

Формулу (1) называюць формулай замены зменнай у нявызначаным інтэграле. Для яе практычнага выкарыстання больш зручным з’яўляецца наступны яе запіс

                              (2)

прычым пры гэтым кажуць, што выкарыстоўваецца метад паднясення пад дыферэнцыял.

Такім чынам, у табліцы інтэгралаў зменную інтэгравання х можна разглядаць як функцыю ад іншай зменнай.

Прыклад 1. Вылічыць .  

►  

або адразу      ◄

 Прыклад 2. Вылічыць .   

► .   ◄

Прыклад 3. Вылічыць .   

►

                                                                                                                  ◄

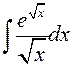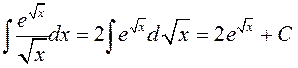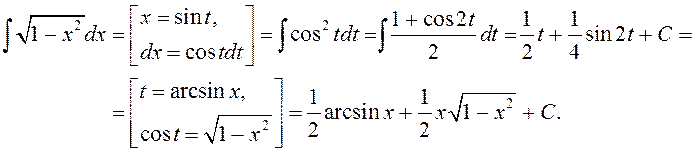
2º. Метад інтэгравання часткамі.

Тэарэма 2. Калі функцыі  – дыферэнцавальныя на інтэрвале Х, а функцыя  мае першаісную на гэтым інтэрвале, то функцыя  таксама мае на Х першаісную, прычым      

.                           (3)

□ Адпаведна правілу дыферэнцавання здабытку маем , адкуль . Паколькі для функцыі  існуе першаісная, а для функцыі  першаіснай з’яўляецца  , то функцыя   таксама мае першаісную, а таму

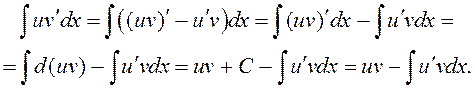
Канстанта С улучана ў нявызначаны інтэграл .  ■

Формулу (3) звычайна выкарыстоўваюць у больш простым выглядзе

                                                 (4)

Прыклад 4. Вылічыць . 

►◄

Прыклад 5. Вылічыць    

► ◄

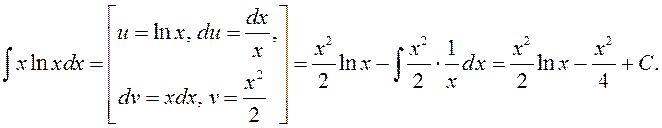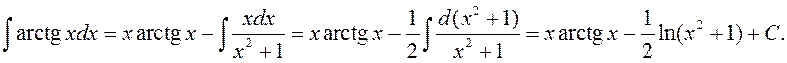Іншы раз формулу інтэгравання часткамі даводзіцца выкарыстоўваць некалькі разоў.

Прыклад 6. Вылічыць  .    

►

◄

     Заўвага 1. Пры вылічэнні інтэгралаў у некаторых выпадках выкарыстоўваюць наступныя прыёмы:

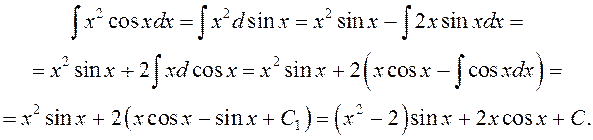1)  у інтэгралах ад функцый      бяруць  – астатні выраз;

2) у інтэгралах ад функцый      бяруць  – астатні множнік;