3º. Калі функцыі ![]() і
і ![]() інтэгравальныя на адрэзку
інтэгравальныя на адрэзку ![]() , то для кожных лікаў α і β
, то для кожных лікаў α і β ![]() функцыя
функцыя ![]() таксама інтэгравальная на
таксама інтэгравальная на ![]() , прычым
, прычым 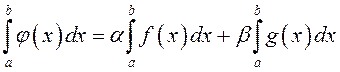 .
.
□ Доказ вынікае з роўнасці для інтэгральных сумаў
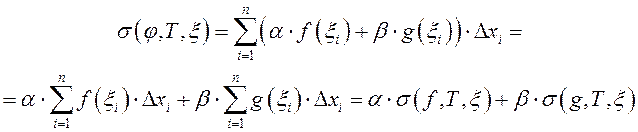
■
Заўвага. Можна даказаць: Калі функцыі ![]() і
і ![]() інтэгравальныя на адрэзку,
то і функцыя
інтэгравальныя на адрэзку,
то і функцыя ![]() інтэгравальная
на гэтым адрэзку.
інтэгравальная
на гэтым адрэзку.
4º. Калі функцыя ![]() інтэгравальная
на
інтэгравальная
на ![]() , то яна інтэгравальная на
, то яна інтэгравальная на ![]() .
.
□ Няхай ![]() – адвольны падзел адрэзка
– адвольны падзел адрэзка ![]() . Разгледзім такі падзел
адрэзка
. Разгледзім такі падзел
адрэзка ![]() , каб на адрэзку
, каб на адрэзку ![]() падзел
падзел ![]() меў тыя ж пункты падзелу,
што і
меў тыя ж пункты падзелу,
што і ![]() і пункты
і пункты
![]() і
і ![]() з’яўляліся пунктамі падзелу
з’яўляліся пунктамі падзелу
![]() , прычым
, прычым ![]() . Адзначым, што
. Адзначым, што ![]() , паколькі ўсе складнікі
неадмоўныя. Такім чынам, маем
, паколькі ўсе складнікі
неадмоўныя. Такім чынам, маем
![]() (1)
(1)
Паколькі ![]() інтэгравальная
на
інтэгравальная
на ![]() , то
, то ![]() пры
пры ![]() і з (1) маем
і з (1) маем ![]() (
(![]() ). Згодна з крытэрам
інтэгравальнасці
). Згодна з крытэрам
інтэгравальнасці ![]() інтэгравальная на
інтэгравальная на
![]() . ■
. ■
5º. (адытыўнасць інтэграла) Калі функцыя ![]() інтэгравальная
на
інтэгравальная
на ![]() , то
, то
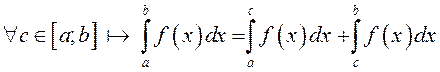 .
.
□ Няхай ![]() і
і
![]() з’яўляюцца адпаведна
падзеламі адрэзкаў
з’яўляюцца адпаведна
падзеламі адрэзкаў ![]() і
і ![]() , а тады
, а тады ![]() ёсць падзел адрэзка
ёсць падзел адрэзка ![]() . Калі
. Калі ![]() ёсць выбарка з падзелу
ёсць выбарка з падзелу ![]() , а
, а ![]() – выбарка з падзелу
– выбарка з падзелу ![]() , то
, то ![]() ёсць выбарка з адрэзку
ёсць выбарка з адрэзку ![]() . З роўнасці
. З роўнасці ![]() , дзе
, дзе ![]() і
і ![]() – інтэгральныя сумы функцыі
– інтэгральныя сумы функцыі
![]() адпаведна на адрэзках
адпаведна на адрэзках ![]() і
і ![]() , а
, а ![]() – інтэгральная сума функцыі
– інтэгральная сума функцыі ![]() на адрэзку
на адрэзку ![]() , вынікае патрэбнае
сцверджанне. ■
, вынікае патрэбнае
сцверджанне. ■
Вынік. Калі
функцыя ![]() інтэгравальная на
інтэгравальная на ![]() , то
, то
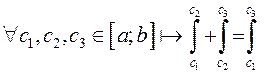 .
.
1º. Калі функцыя ![]() інтэгравальная на
інтэгравальная на
![]() і
і ![]() , то
, то 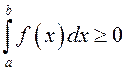 .
.
□ Паколькі пры кожным падзеле ![]() адрэзка
адрэзка ![]() і кожнай выбарцы
і кожнай выбарцы ![]() мае месца
мае месца 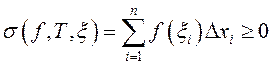 , то пасля пераходу да
ліміту пры
, то пасля пераходу да
ліміту пры ![]() атрымаем патрэбнае
сцверджанне. ■
атрымаем патрэбнае
сцверджанне. ■
Вынік (манатоннасць інтэграла). Калі функцыі ![]() і
і ![]() інтэгравальныя на
інтэгравальныя на ![]() і
і ![]() , то
, то  .
.
□ Для функцыі ![]() праўдзяцца
ўмовы з 1º. Таму
праўдзяцца
ўмовы з 1º. Таму
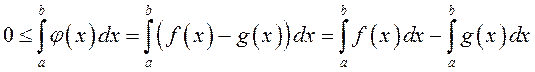 ,
,
адкуль атрымліваецца патрэбная няроўнасць. ■
Заўвага. Калі функцыя ![]() інтэгравальная
на
інтэгравальная
на ![]() ,
, ![]() і існуе пункт
і існуе пункт ![]() , а функцыя
, а функцыя ![]() непарыўная ў пункце
непарыўная ў пункце ![]() , то
, то 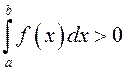 .
.
2º. (інтэгравальнасць модуля) Калі функцыя ![]() інтэгравальная
на
інтэгравальная
на ![]() , то функцыя
, то функцыя ![]() таксама інтэгравальная на
таксама інтэгравальная на ![]() , прычым
, прычым 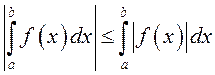 .
.
□ Разгледзім функцыю ![]() – непарыўную на ўсёй
лікавай прамой. Таму функцыя
– непарыўную на ўсёй
лікавай прамой. Таму функцыя ![]() інтэгравальная
на
інтэгравальная
на ![]() згодна з тэарэмаю пра
інтэгравальнасць складанай функцыі. З няроўнасці
згодна з тэарэмаю пра
інтэгравальнасць складанай функцыі. З няроўнасці
![]()
на падставе ўласцівасці манатоннасці інтэграла і з інтэгравальнасці функцый маем
 . ■
. ■
Заўвага. Калі функцыя ![]() інтэгравальная
на адрэзку з канцамі
інтэгравальная
на адрэзку з канцамі ![]() і
і ![]() (г.зн. або
(г.зн. або ![]() , або
, або ![]() ), то праўдзіцца няроўнасць
), то праўдзіцца няроўнасць 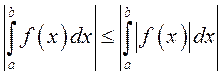 .
.
3º. Калі функцыя ![]() інтэгравальная
і абмежаваная на
інтэгравальная
і абмежаваная на ![]() , г.зн.
, г.зн. ![]() , то
, то 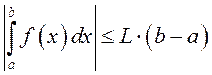 .
.
□ З інтэгравальнасці модуля і ўласцівассці манатоннасці інтэграла вынікае
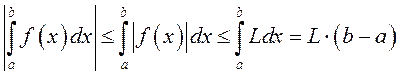 . ■
. ■
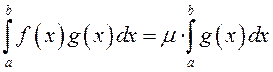 . (1)
. (1)
□ Няхай ![]() .
Паколькі
.
Паколькі ![]() інтэгравальная
на
інтэгравальная
на ![]() , то яна абмежаваная
на
, то яна абмежаваная
на ![]() , а г. зн.
, а г. зн. ![]() . Пры гэтым маем
. Пры гэтым маем ![]() . Адсюль, паколькі
. Адсюль, паколькі ![]() , маем
, маем
![]()
Паколькі ![]() ёсць
інтэгравальная на
ёсць
інтэгравальная на ![]() ,
то згодна з уласцівасцю манатоннасці інтэграла маем
,
то згодна з уласцівасцю манатоннасці інтэграла маем
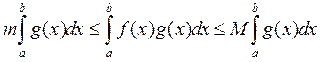 .
(2)
.
(2)
Калі пры гэтым 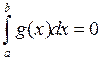 ,
то
,
то 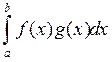 таксама роўны нулю і
роўнасць (1) праўдзіцца пры кожным
таксама роўны нулю і
роўнасць (1) праўдзіцца пры кожным ![]() .
.
Калі ж 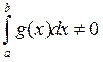 ,
то
,
то 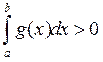 , і няроўнасць (2) можна
падзяліць на гэты
, і няроўнасць (2) можна
падзяліць на гэты
інтэграл. Атрымаем 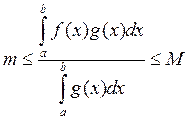 .
Абазначым
.
Абазначым 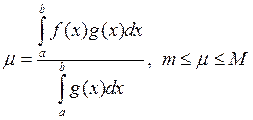 . З гэтай роўнасці і
атрымліваецца (1).
. З гэтай роўнасці і
атрымліваецца (1).
Калі ж ![]() ,
то для функцыі
,
то для функцыі ![]() мае месца (1),
г. зн.
мае месца (1),
г. зн.
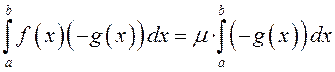 .
.
Дамнажаючы абедзве часткі гэтай роўнасці на –1, атрымаем (1). ■
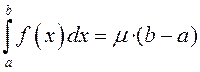 .
. □ Калі ў тэарэме 1 узяць ![]() , то атрымаем
, то атрымаем 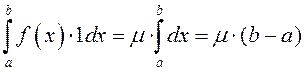 ■
■
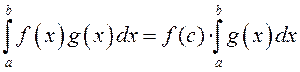 . (3)
. (3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.