Нявызначаны інтэграл. Азначэнне і ўласцівасці нявызначанага інтэграла. Азначэнне нявызначанага інтэграла, страница 3

3) Калі ж , то . Пры гэтым выкарыстоўваюць падстановы Эйлера:  і  .

Сапраўды,

,

,

.

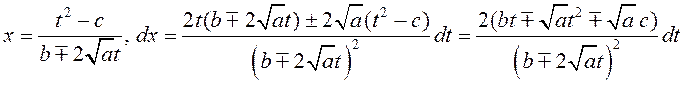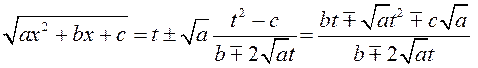Такім чынам,

Аналагічна выконваецца другая падстанова Эйлера.

Прыклад 5. Вылічыць .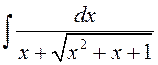

►Выканаем першую падстанову Эйлера , прычым выбіраем знак “–“, паколькі пры гэтым . Далей маем

.

=

◄

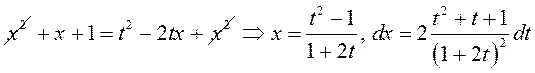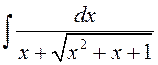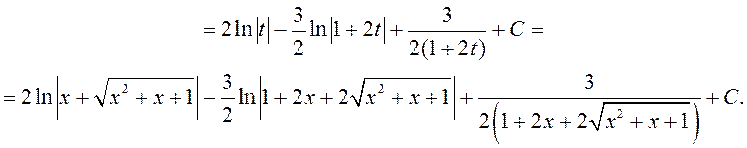
Разгледзім два прыватныя выпадкі квадратовай ірацыянальнасці.

А) 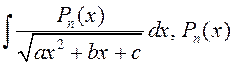 – мнагасклад ступені . Інтэграл будзем шукаць, зыходзячы з роўнасці

дзе  – мнагасклад ступені  з нявызначанымі каэфіцыентамі,  – невядомая канстанта. Пасля дыферэнцавання гэтай роўнасці атрымаем

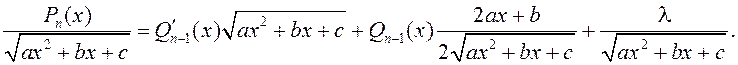
Дамнажаючы абедзве часткі на , прыходзім да роўнасці

Метадам адпаведных каэфіцыентаў знойдзем мнагасклад  і лік .

Прыклад 6. Вылічыць .

►Інтэграл можна вылічыць метадам замены зменнай: 1) ; 2) ; 3) . Правядзем вылічэнне інтэграла метадам нявызначаных каэфіцыентаў.

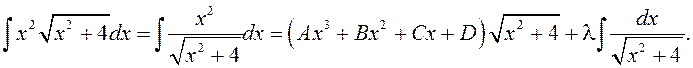
Пасля дыферэнцавання маем

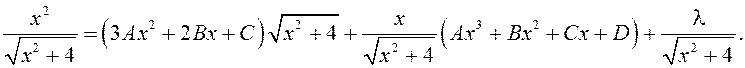
Дамнажаючы абедзве часткі роўнасці на , маем

Метадам адпаведных каэфіцыентаў прыходзім да сістэмы:

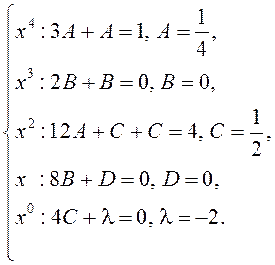
Такім чынам,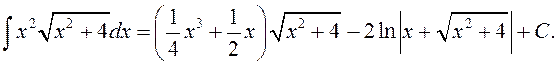

Б) 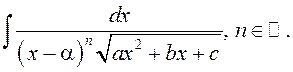 Зробім замену . Атрымаем

Атрымалі інтэграл тыпу А).

Прыклад 7.

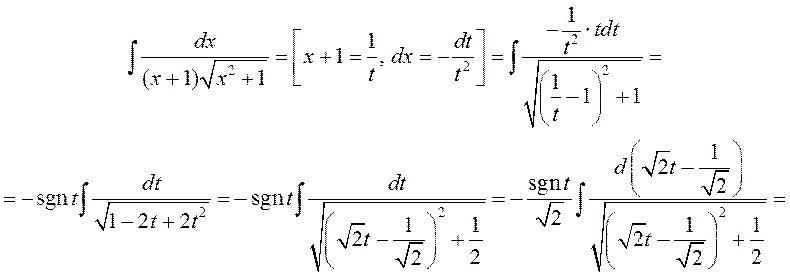
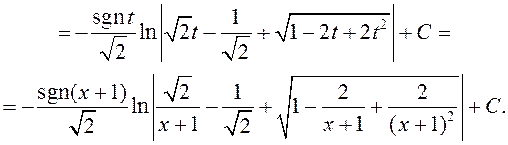
4º. Інтэграванне біномнага дыферэнцыяла.

Пры вылічэнні інтэграла  маюць месца тры выпадкі інтэгравальнасці.

1) . Няхай пры гэтым . Падынтэгральная функцыя ёсць дробава-лінейная ірацыянальнасць , дзе  – найменшы супольны кратны назоўнікаў лікаў  і . Падстанова  рацыяналізуе падынтэгральную функ-цыю.

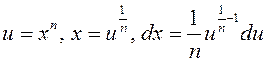2) . Зробім замену  і атрымаем . Калі , то падынтэгральная функцыя ёсць дробава-лінейная ірацыянальнасць , а таму падстанова  рацы-яналізуе інтэграл ад апошняй функцыі. Такім чынам, падстанова  рацыяналізуе зыходны інтэграл.

3) . Пасля замены  атрымаем інтэграл

.

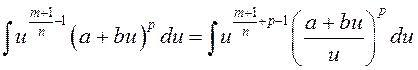Падынтэгральная функцыя ёсць 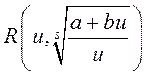, дзе  – назоўнік рацыянальнага ліку . Такім чынам, падстанова .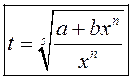

Расійскі матэматык Чабышоў даказаў, што ў іншых выпадках інтэграл не вылічаецца ў элементарных функцыях.

Назавем іншыя інтэгралы, якія не вылічаюцца ў элементарных функцыях.

 – інтэграл Пуасона;  – інтэгралы Фрэнэля;

 – інтэгральны лагарыфм;  – інтэгралы Дырыхле.

§4.5. Азначэнне і ўмовы існавання вызначанага інтэграла.

Няхай функцыя  вызначана на адрэзку  (магчыма разрыўная, магчыма непарыўная, магчыма недыферэнцавальная, магчыма дыферэнцавальная ў пунктах адрэзка). Няхай  – сукупнасць пунктаў гэтага адрэзка такіх, што . Мноства гэтых пунктаў назавем падзелам адрэзка  і абазначым . Адрэзкі  назавем адрэзкамі падзелу , або частковымі адрэзкамі адрэзка .

Абазначым праз  даўжыні адрэзкаў . Лік  назавем дробнасцю падзелу  . Мноства пунктаў  будзем называць выбаркай з адрэзка . Суму 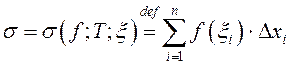 будзем называць інтэгральнаю сумай для функцыі  пры зададзеным падзеле  і фіксаванай выбарцы .

def. Лік I называюць вызначаным інтэгралам функцыі  на адрэзку  і абазначаюць 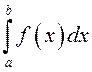 , калі

             (1)

Пры гэтым таксама кажуць, што існуе ліміт  інтэгральных сумаў пры , і гэты ліміт не залежыць ні ад падзелу , ні ад выбаркі  і пішуць 

Калі існуе лік , які вызначаецца ўмоваю (1), то функцыю  называюць інтэгравальнаю паводле Рымана на адрэзку  і пры гэтым кажуць таксама, што існуе інтэграл ад функцыі  на адрэзку .

Такім чынам, функцыя ёсць інтэгравальная на адрэзку пры ўмове існавання ліміту інтэгральных сумаў, калі дробнасць падзелу адрэзка імкнецца да нуля, і гэты ліміт не залежыць ні ад падзелу, ні ад выбаркі.

Прыклад 1. Вылічыць      

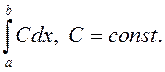
► Паколькі , то , а таму  .◄

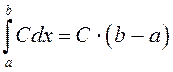Вызначаны інітэграл мае просты геаметрычны сэнс. Няхай функцыя  ёсць неадмоўная і непарыўная на адрэзку . Тады інтэгральная сума  раўняецца плошчы “прыступкавай фігуры” (гл. рысунак).

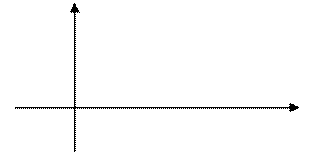
Фігуру G, абмежаваную адрэзкамі прамых  і графікам функцыі  , г. зн. , будзем называць крывалінейнаю трапецыяй.

Фігуру G, абмежаваную адрэзкамі прамых  і графікам функцыі  , г. зн. , будзем называць крывалінейнаю трапецыяй.