►Сапраўды, 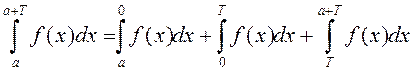 . У апошнім інтэграле зробім замену
. У апошнім інтэграле зробім замену 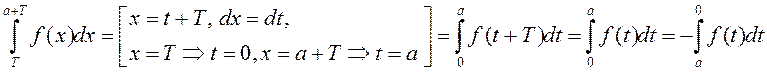 . Падстаўляючы ў папярэдні
выраз, атрымаем
. Падстаўляючы ў папярэдні
выраз, атрымаем
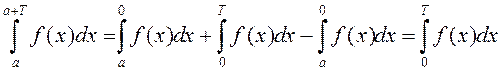 . ◄
. ◄
4º. Інтэграванне часткамі.
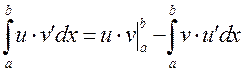 .
.□ З роўнасці ![]() маем
маем
![]() . Інтэгруючы апошнюю
роўнасць на
. Інтэгруючы апошнюю
роўнасць на ![]() , маем
, маем 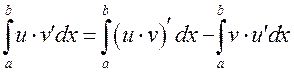 ,
што раўназначна формуле, якую трэба было даказаць. ■
,
што раўназначна формуле, якую трэба было даказаць. ■
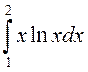 .
. ► Карыстаючыся формулаю інтэгравання часткамі,
маем
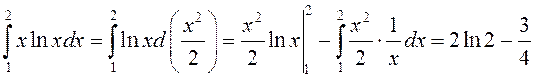 .◄
.◄
1º.Плошча плоскай фігуры.
Адвольнае абмежаванае мноства пунктаў плоскасці будзем называць плоскаю фігурай.
1.1) Плоскую фігуру ![]() называюць крывалінейнаю трапецыяй.
называюць крывалінейнаю трапецыяй.
![]()
Няхай ![]() ёсць падзел
адрэзка
ёсць падзел
адрэзка ![]() з дробнасцю
з дробнасцю ![]() ,
а
,
а ![]() і
і ![]() – адпаведна верхняя і ніжняя
сумы Дарбу.
– адпаведна верхняя і ніжняя
сумы Дарбу.
![]()
З рысунка відаць, што ![]() ,
дзе
,
дзе ![]() – плошча крывалінейнай трапецыі
– плошча крывалінейнай трапецыі
![]() . Паколькі згодна з крытэрам
інтэгравальнасці функцыі
. Паколькі згодна з крытэрам
інтэгравальнасці функцыі 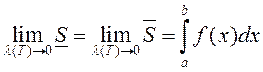 , то і
плошчу крывалінейнай трапецыі
, то і
плошчу крывалінейнай трапецыі ![]() будзем
лічыць роўнай значэнню гэтага інтэграла, г. зн.
будзем
лічыць роўнай значэнню гэтага інтэграла, г. зн. 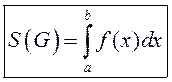 .
.
Калі плоская фігура ![]() задаецца ўмоваю
задаецца ўмоваю ![]() то плошча гэтай фігуры
роўная розніцы плошчаў крывалінейных трапецыяў
то плошча гэтай фігуры
роўная розніцы плошчаў крывалінейных трапецыяў ![]() і
і
![]() .
.
![]()
Таму 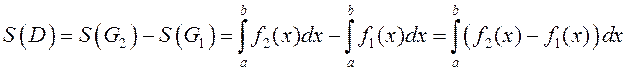 .
.
Такім чынам, 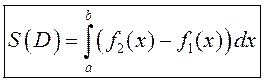 .
.
Зазначым, што гэтая формула застаецца
праўдзіваю і ў тым выпадку, калі функцыі ![]() і
і
![]() не з’яўляюцца неадмоўнымі.
не з’яўляюцца неадмоўнымі.
Сапраўды, калі ![]()
![]()
то з абмежаванасці функцый ![]() і
і
![]() (Чаму?) вынікае існаванне
такога ліку
(Чаму?) вынікае існаванне
такога ліку ![]() , што
, што ![]() . Паколькі
. Паколькі 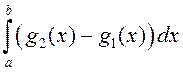 выражае плошчу новай
фігуры, якая атрымліваецца пры дапамозе паралельнага пераносу фігуры
выражае плошчу новай
фігуры, якая атрымліваецца пры дапамозе паралельнага пераносу фігуры ![]() , то і плошча фігуры
, то і плошча фігуры ![]() роўная гэтаму інтэгралу.
Пры гэтым маем
роўная гэтаму інтэгралу.
Пры гэтым маем 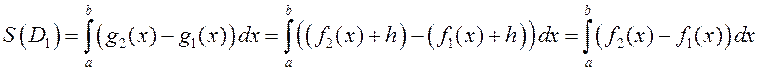 .
.
►
![]()
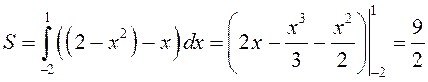 .◄
.◄
1.2)
Няхай крывая зададзена ў палярнай сістэме каардынатаў ![]() , дзе
, дзе ![]() – непарыўная функцыя.
Плоскую фігуру
– непарыўная функцыя.
Плоскую фігуру ![]() будзем
называць крывалінейным сектарам.
будзем
называць крывалінейным сектарам.
![]()
Няхай ![]() –
некаторы падзел адрэзку
–
некаторы падзел адрэзку ![]() з
дробнасцю падзела
з
дробнасцю падзела ![]() , а
, а ![]() – некаторая выбарка пунктаў
– некаторая выбарка пунктаў ![]() . Паколькі плошча кругавога
сектара з радыюсам
. Паколькі плошча кругавога
сектара з радыюсам ![]() , які змяшчае
цэнтральны вугал
, які змяшчае
цэнтральны вугал ![]() , роўная
, роўная 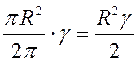 [атрымліваецца з прапорцыі
[атрымліваецца з прапорцыі 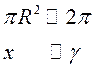 ], то плошча крывалінейнага
сектара набліжана роўная
], то плошча крывалінейнага
сектара набліжана роўная 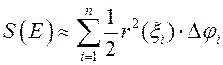 , дзе
, дзе ![]() . Калі
. Калі ![]() , то
, то 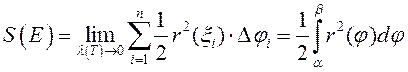 . Такім чынам
. Такім чынам
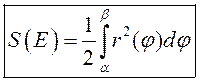
![]()
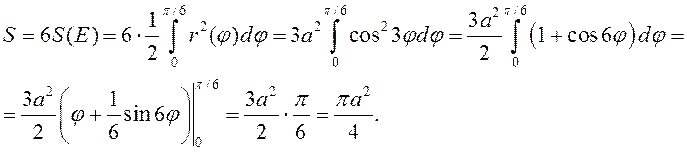 ◄
◄
1.3) Для вылічэння плошчы крывалінейнай трапецыі, калі яе верхняя мяжа
зададзена параметрычна ![]() , прычым
, прычым
![]() , (тут важна
, (тут важна ![]() , гэта будзе, калі
, гэта будзе, калі ![]() ) трэба ў формуле
) трэба ў формуле 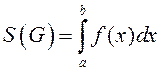 зрабіць замену зменнай
зрабіць замену зменнай ![]() . Пры гэтым
. Пры гэтым ![]() . Атрымаем
. Атрымаем 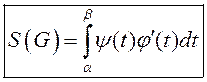 .
.
► Эліпс сіметрычны да абедзвюх восяў каардынатаў, таму
![]()
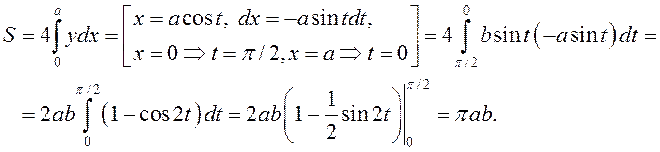
У прыватнасці, калі ![]() , атрымаем вядомую формулу
плошчы круга
, атрымаем вядомую формулу
плошчы круга ![]() .◄
.◄
2º. Даўжыня крывой.
2.1) Разгледзім плоскую крывую ![]() , дзе
, дзе ![]() – непарыўная на
– непарыўная на ![]() функцыя. Няхай
функцыя. Няхай ![]() – адвольны па-дзел адрэзка
– адвольны па-дзел адрэзка ![]() . Крывую
. Крывую ![]() падзе-лім пунктамі
падзе-лім пунктамі ![]() . Злучым суседнія пункты
хордамі і атрымаем умежаную ў крывую
. Злучым суседнія пункты
хордамі і атрымаем умежаную ў крывую ![]() ламаную,
якую абазначым
ламаную,
якую абазначым ![]() .
.
![]()
Няхай ![]() –
даўжыня хорды
–
даўжыня хорды ![]() гэтай ламанай,
гэтай ламанай, ![]() – даўжыня найбольшай з
хордаў, а
– даўжыня найбольшай з
хордаў, а 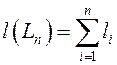 – даўжыня ламанай
– даўжыня ламанай ![]() .
.
def. Лік ![]() называецца даўжынёй крывой
называецца даўжынёй крывой ![]() і абазначаецца
і абазначаецца ![]() ,
калі
,
калі ![]() . Пры гэтым кажуць, што лік
. Пры гэтым кажуць, што лік ![]() ёсць ліміт даўжыняў
ламаных
ёсць ліміт даўжыняў
ламаных ![]() , умежаных у
крывую
, умежаных у
крывую ![]() пры
пры ![]() і пішуць
і пішуць ![]() . Крывую, якая мае дўжыню,
называюць выпрастальнаю.
. Крывую, якая мае дўжыню,
называюць выпрастальнаю.
Дапусцім, што ![]() мае
на
мае
на ![]() непарыўную вытворную
(г. зн. крывая гладкая). Няхай
непарыўную вытворную
(г. зн. крывая гладкая). Няхай ![]() –
пункты падзелу крывой,
–
пункты падзелу крывой, ![]()
![]() . Тады
. Тады ![]() , а
, а
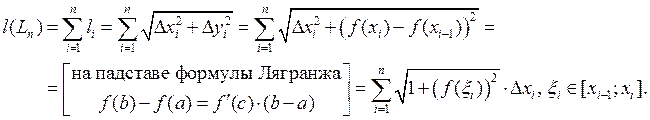
Калі ![]() ,
а таму
,
а таму
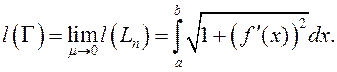 (1)
(1)
2.2) Няхай гладкая крывая ![]() зададзена
параметрычна
зададзена
параметрычна ![]() ,
, ![]() , прычым
, прычым ![]() – непарыўныя на
– непарыўныя на ![]() і
і ![]() (у кожным пункце крывой
(у кожным пункце крывой ![]() павінна існаваць
вытворная), г. зн.
павінна існаваць
вытворная), г. зн. ![]() –
манатонная. А паколькі
–
манатонная. А паколькі ![]() , то
, то ![]() – нарастальная, г. зн.
– нарастальная, г. зн. ![]() . Калі ў (1) зрабіць замену
. Калі ў (1) зрабіць замену ![]() , атрымаем
, атрымаем
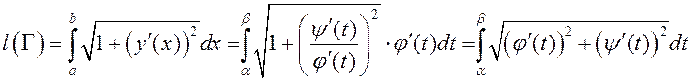 .
.
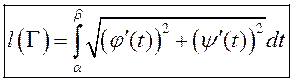 (2)
(2)
Заўвага. Непарыўная крывая можа быць кавалкава-гладкаю. Тады яе даўжыня – сума даўжыняў гладкіх кавалкаў.
Калі ![]() , то
, то 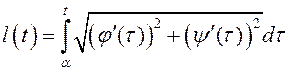 ,
,
![]() .
.
Атрымалі так званую формулу дыферэнцыяла дугі ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.