Відавочна, што пры дастаткова дробным падзеле
адрэзка ![]() “прыступкавая фігура” мала
чым адрозніваецца ад крывалінейнай трапецыі, а таму , калі функцыя
“прыступкавая фігура” мала
чым адрозніваецца ад крывалінейнай трапецыі, а таму , калі функцыя ![]() ёсць інтэгравальная на
ёсць інтэгравальная на ![]() , то
, то 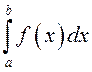 азначае плошчу крывалінейнай трапецыі:
азначае плошчу крывалінейнай трапецыі:
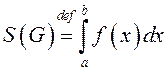 .
.
►
Падзелім адрэзак ![]() на n роўных (дзеля зручнасці)
частак. Маем
на n роўных (дзеля зручнасці)
частак. Маем ![]() , а таму
, а таму ![]() , калі
, калі ![]() . Выбіраючы
. Выбіраючы ![]() , возьмем правыя канцы
адрэзкаў
, возьмем правыя канцы
адрэзкаў ![]() , г.зн.
, г.зн. ![]() . Вылічым інтэгральную суму
. Вылічым інтэгральную суму 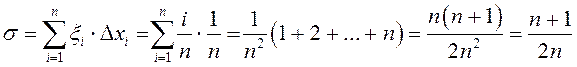 . Адкуль
. Адкуль
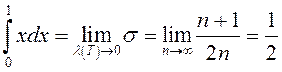 . (Ці
з’яўляецца значэнне гэтага ліміта значэннем адпаведнага інтэграла?)◄
. (Ці
з’яўляецца значэнне гэтага ліміта значэннем адпаведнага інтэграла?)◄
□ Паколькі ![]() ёсць
інтэгравальная на
ёсць
інтэгравальная на ![]() то
існуе лік I , які адпавядае ўмове (1) , г.зн. пры
то
існуе лік I , які адпавядае ўмове (1) , г.зн. пры ![]() маем няроўнасць
маем няроўнасць
![]() ,
(2)
,
(2)
якая праўдзіцца пры кожным падзеле ![]() і пры кожнай выбарцы
і пры кожнай выбарцы ![]() .
.
Зафіксуем падзел ![]() і
дапусцім процілеглае, што функцыя
і
дапусцім процілеглае, што функцыя ![]() неабмежаваная
на
неабмежаваная
на ![]() .
Тады функцыя неабмежаваная прынамсі на адным з адрэзкаў
.
Тады функцыя неабмежаваная прынамсі на адным з адрэзкаў ![]() падзелу
падзелу ![]() . Не парушаючы агульнасці,
будзем лічыць, што
. Не парушаючы агульнасці,
будзем лічыць, што ![]() неабмежаваная на
адрэзку
неабмежаваная на
адрэзку ![]() . Зафіксуем пункты
. Зафіксуем пункты ![]() і абазначым
і абазначым 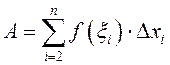 . Тады
. Тады ![]() і адпаведна няроўнасці (2),
маем няроўнасць
і адпаведна няроўнасці (2),
маем няроўнасць
![]() , якая праўдзіцца
, якая праўдзіцца ![]() .
Паколькі
.
Паколькі ![]() , то няроўнасць
, то няроўнасць
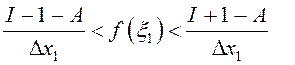
праўдзівая ![]() . Гэта
значыць, што функцыя
. Гэта
значыць, што функцыя ![]() абмежаваная на
адрэзку
абмежаваная на
адрэзку ![]() , што супярэчыць дапушчэнню
неабмежаванасці
, што супярэчыць дапушчэнню
неабмежаванасці ![]() на
на ![]() . ■
. ■
Напрыклад, функцыя Дырыхле
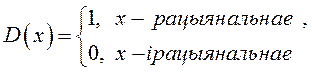
на адрэзку ![]() абмежаваная, але
неінтэгравальная, бо пры
абмежаваная, але
неінтэгравальная, бо пры ![]() рацыянальных
рацыянальных
![]() , а пры
, а пры ![]() ірацыянальных
ірацыянальных ![]() .
.
Няхай ![]() абмежаваная
на
абмежаваная
на ![]() , і
, і ![]() – некаторы падзел адрэзка
– некаторы падзел адрэзка ![]() . Няхай
. Няхай
![]() .(Ці існуюць?)
.(Ці існуюць?)
Сумы 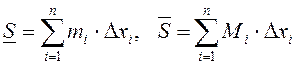 называюцца адпаведна ніжняй
і верхняй
называюцца адпаведна ніжняй
і верхняй
сумамі Дарбу для дадзенага падзелу ![]() .
.
Паколькі ![]() ,
то
,
то 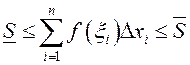 , г.зн.
, г.зн. ![]() .
.
Мае месца
Калі абазначыць ![]() так
званае ваганне функцыі
так
званае ваганне функцыі ![]() на адрэзку
на адрэзку ![]() , то
розніцу
, то
розніцу
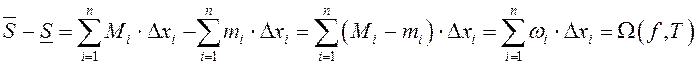
называюць інтэгральным ваганнем функцыі ![]() на адрэзку
на адрэзку ![]() .
.
Такім чынам, умова крытэра інтэгравальнасці ёсць
![]() .
.
Функцыя ![]() называецца
раўнамерна непарыўнаю на мностве
называецца
раўнамерна непарыўнаю на мностве ![]() ,калі
,калі
![]() . (1)
. (1)
Згодна з тэарэмай Кантара, калі функцыя непарыўная на адрэзку, то яна раўнамерна непарыўная на гэтым адрэзку.
□ Няхай функцыя ![]() ёсць
непарыўная на адрэзку
ёсць
непарыўная на адрэзку ![]() . Паводле тэарэмы
Кантара яна раўнамерна непарыўная на гэтым адрэзку, г.зн. мае месца (1).
. Паводле тэарэмы
Кантара яна раўнамерна непарыўная на гэтым адрэзку, г.зн. мае месца (1).
Няхай ![]() – такі
падзел адрэзка
– такі
падзел адрэзка ![]() , што яго
дробнасць
, што яго
дробнасць ![]() . Адпаведна другой тэарэме
Ваерштраса
. Адпаведна другой тэарэме
Ваерштраса
![]() .
.
Паколькі ![]() , а
, а ![]() , то
, то ![]()
![]() ,
а таму
,
а таму ![]() . Маем
. Маем
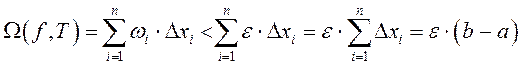 .
.
Згодна з крытэрам інтэгравальнасці функцыя ![]() ёсць інтэгравальная на
ёсць інтэгравальная на ![]() . ■
. ■
Можна даказаць праўдзівасць наступных тэарэм:
1º. 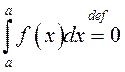 – натуральнае пашырэнне
паняцця інтэграла на адрэзак нулявой даўжыні.
– натуральнае пашырэнне
паняцця інтэграла на адрэзак нулявой даўжыні.
2º. 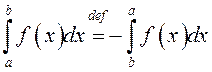 – тут
– тут ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.