►
![]()
Маем раўнанне цыклоіды ![]()
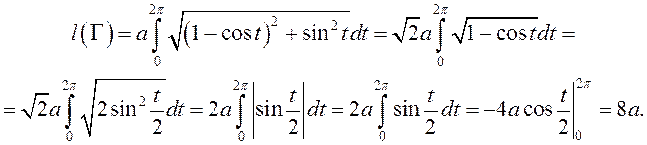 ◄
◄
2.3) Калі крывая зададзена ў палярных каардынатах ![]() , прычым
, прычым ![]() – непарыўная, то, ўлічваючы
– непарыўная, то, ўлічваючы ![]() , маем параметрычнае заданне
крывой
, маем параметрычнае заданне
крывой ![]() . Паколькі
. Паколькі
![]() , то
, то ![]() . З
формулы (2) маем
. З
формулы (2) маем
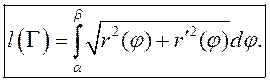
3º. Аб’ём цела авароту.
Разгледзім цела ,
якое атрымліваецца аваротам крывалінейнай трапецыі ![]() вакол
восі
вакол
восі ![]() , дзе функцыя
, дзе функцыя ![]() непарыўная на
непарыўная на ![]() .
.
![]()
Няхай ![]() – некаторы падзел адрэзка
– некаторы падзел адрэзка ![]() з дробнасцю падзела
з дробнасцю падзела ![]() . На кожным адрэзку
. На кожным адрэзку ![]() пабудуем прамавугольнік
пабудуем прамавугольнік
![]()
Кожны прамавугольнік ![]() пры авароце вакол восі
пры авароце вакол восі ![]() утворыць цыліндр, аб’ём
якога
утворыць цыліндр, аб’ём
якога ![]() . Тады аб’ём
. Тады аб’ём ![]() цела, атрыманага аваротам
трапецыі
цела, атрыманага аваротам
трапецыі ![]() вакол восі
вакол восі ![]() , набліжана роўны
, набліжана роўны 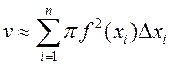 . Гэтую суму можна
разглядаць як інтэгральную суму для функцыі
. Гэтую суму можна
разглядаць як інтэгральную суму для функцыі ![]() з
падзелам
з
падзелам ![]() і выбаркай
і выбаркай ![]() . Паколькі
. Паколькі ![]() ёсць непарыўная на
ёсць непарыўная на ![]() , то ліміт інтэгральнай сумы
існуе і
, то ліміт інтэгральнай сумы
існуе і 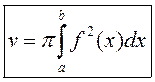 .
.
Заўвага. Калі праекцыя цела ![]() на
вось
на
вось ![]() ёсць адрэзак
ёсць адрэзак ![]() і
і ![]() фігура, якая атрымліваецца
пры перасячэнні цела
фігура, якая атрымліваецца
пры перасячэнні цела ![]() плоскасцю
плоскасцю ![]() , мае плошчу
, мае плошчу ![]() , то аб’ём цела вылічаецца
паводле формулы
, то аб’ём цела вылічаецца
паводле формулы 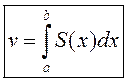 .
.
► Паколькі раўнанне акружыны ![]() , то
, то
![]()
![]() . Маем
. Маем 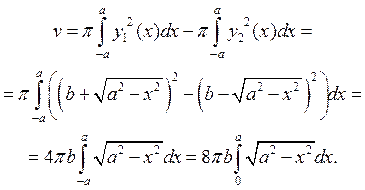
Апошні інтэграл роўны плошчы чвэрці круга з радыюсам ![]() . Таму
. Таму ![]() .◄
.◄
4º. Работа зменнай сілы.
Няхай матэрыяльны пункт перамяшчаецца пад
уздзеяннем сілы ![]() , якая накіраваная
ўздоўж восі
, якая накіраваная
ўздоўж восі ![]() і мае зменную велічыню
і мае зменную велічыню ![]() , непарыўную на
, непарыўную на ![]() . Патрабуецца вызначыць
работу
. Патрабуецца вызначыць
работу ![]() , якая ствараецца сілай
, якая ствараецца сілай ![]() пры перамяшчэнні
матэрыяльнага пункта ўздоўж восі
пры перамяшчэнні
матэрыяльнага пункта ўздоўж восі ![]() з пункта
з пункта
![]() у пункт
у пункт ![]() .
.
Возьмем некаторы падзел ![]() адрэзка
адрэзка ![]() з дробнасцю падзелу
з дробнасцю падзелу ![]() і выбаркаю
і выбаркаю ![]() . Калі адрэзак
. Калі адрэзак ![]() малы, то змяненне сілы
ўздоўж яго нязначнае, а таму работа на адрэзку
малы, то змяненне сілы
ўздоўж яго нязначнае, а таму работа на адрэзку ![]() набліжана
роўная
набліжана
роўная ![]() . Работа на адрэзку
. Работа на адрэзку ![]() набліжана роўная
набліжана роўная ![]() . Паколькі
. Паколькі ![]() непарыўная на
непарыўная на ![]() , то пры
, то пры ![]() маем
маем 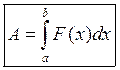 .
.
Прыклад 6.
Вылічыць работу ![]() , неабходную для
запуску цела масаю
, неабходную для
запуску цела масаю ![]() з паверхні зямлі
вертыкальна ўверх на вышыню
з паверхні зямлі
вертыкальна ўверх на вышыню ![]() .
.
► Няхай ![]() –
сіла прыцяжэння цела зямлёю,
–
сіла прыцяжэння цела зямлёю, ![]() – маса
зямлі, а
– маса
зямлі, а ![]() – яе радыюс.
– яе радыюс.
Адпаведна закону сусветнага
прыцяжэння ![]() .
.
Абазначым ![]() , маем
, маем ![]() . Калі
. Калі ![]() , то сіла
, то сіла ![]() роўная вазе цела
роўная вазе цела ![]() , г. зн.
, г. зн. ![]() . Такім чынам,
. Такім чынам, ![]() , а таму работа
, а таму работа ![]() будзе роўная
будзе роўная
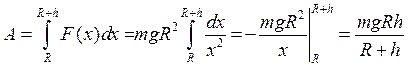 . ◄
. ◄
Няхай функцыя ![]() ёсць вызначаная
ёсць вызначаная ![]() і інтэгравальная на адрэзку
і інтэгравальная на адрэзку
![]() .
.
def. Ліміт 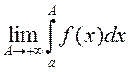 называюць неўласцівым
інтэгралам ад функцыі
называюць неўласцівым
інтэгралам ад функцыі ![]() на бясконцым прамежку
на бясконцым прамежку ![]() ,
або неўласцівым інтэгралам першага роду (НІ-1) і
абазначаюць
,
або неўласцівым інтэгралам першага роду (НІ-1) і
абазначаюць
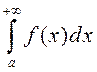
![]()
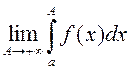 .
(1)
.
(1)
Калі існуе канечны ліміт (1),
то НІ-1 называецца збежным, а функцыя ![]() – інтэгравальнаю ў неўласцівым
сэнсе на прамежку
– інтэгравальнаю ў неўласцівым
сэнсе на прамежку ![]() . Калі ж
ліміт (1) не існуе, то НІ-1 называецца разбежным, а калі
ён пры гэтым ёсць бясконца вялікі, то пішуць
. Калі ж
ліміт (1) не існуе, то НІ-1 называецца разбежным, а калі
ён пры гэтым ёсць бясконца вялікі, то пішуць 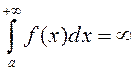 .
.
Неўласцівы інтэграл па
бясконцым прамежку ![]() азначаецца
аналагічна
азначаецца
аналагічна
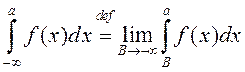 ,
,
а калі ён разглядаецца на ўсёй лікавай прамой, то
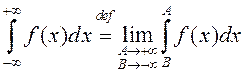 , прычым ліміт не залежыць ад
таго, як
, прычым ліміт не залежыць ад
таго, як ![]() і
і ![]() імкнуцца да
імкнуцца да ![]() і
і ![]() .
.
|
Калі |
|
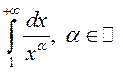 .
. ► 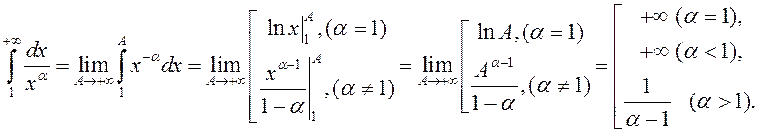
Такім чынам, пры ![]() інтэграл збежны, пры
інтэграл збежны, пры ![]() – разбежны.◄
– разбежны.◄
На падставе ўласцівасцяў лімітаў і вызначаных інтэгралаў атрымліваюцца наступныя ўласцівасці НІ-1.
1º. Калі збягаюцца інтэгралы 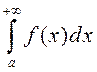 і
і 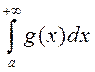 , то
, то ![]() збягаецца інтэ-грал
збягаецца інтэ-грал 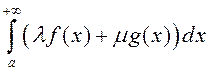 , прычым
, прычым 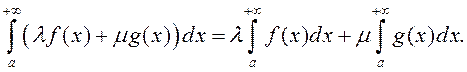
2º. Калі функцыя ![]() непарыўная
непарыўная ![]() і
і
![]() – яе непарыўная перша-існая,
то
– яе непарыўная перша-існая,
то 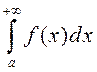 ёсць збежны, калі і толькі
калі існуе
ёсць збежны, калі і толькі
калі існуе ![]() , прычым
, прычым
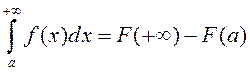 .
.
Гэта вынікае з формулы
Ньютана-Ляйбніца 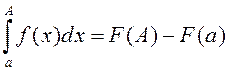 .
.
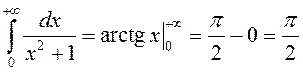 .
. 3º. Калі 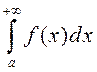 ёсць збежны, то
ёсць збежны, то ![]()
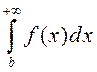 таксама
збежны, прычым
таксама
збежны, прычым
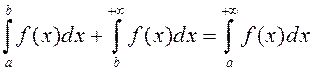 .
.
4º. Калі функцыя ![]() непарыўная на
непарыўная на ![]() ,
а функцыя
,
а функцыя ![]() непарыўна дыферэнцавальная
на
непарыўна дыферэнцавальная
на ![]() , манатонная і задавальняе
умовы
, манатонная і задавальняе
умовы ![]() , то праўдзіцца формула
, то праўдзіцца формула
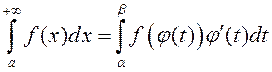
пры умове існавання прынамсі аднаго з гэтых інтэгралаў.
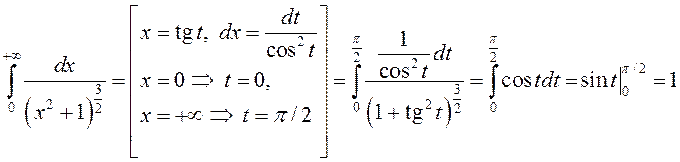 .
.
5º. Збежнасць НІ-1 раўназначная існаванню ліміта функцыі
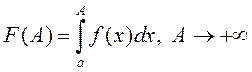 .
(2)
.
(2)
Адпаведна крытэру Кашы існавання ліміту функцыі маем:
![]() існуе,
калі і толькі калі
існуе,
калі і толькі калі ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.