□ Для функцыый f
і g
мае месца формула (1). Паколькі f
непарыўная на ![]() , то
, то ![]() . На падставе другой тэарэмы
Ваерштраса
. На падставе другой тэарэмы
Ваерштраса ![]() . Паколькі
. Паколькі ![]() , то згодна з тэарэмаю
Бальцана-Кашы аб прамежкавым значэнні непарыўнай функцыі
, то згодна з тэарэмаю
Бальцана-Кашы аб прамежкавым значэнні непарыўнай функцыі ![]() . Падстаўляючы ў (1) замест
. Падстаўляючы ў (1) замест ![]() значэнне
значэнне ![]() , атрымаем (3). ■
, атрымаем (3). ■
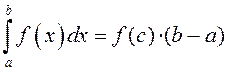 .
.
□ Калі ў тэарэме 2 узяць ![]() , то атрымаем
, то атрымаем
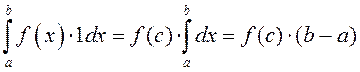 ■
■
Калі функцыя ![]() ёсць
інтэгравальная на
ёсць
інтэгравальная на ![]() , то
, то ![]() існуе інтэграл
існуе інтэграл
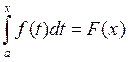 ,
(1)
,
(1)
які называюць інтэгралам са зменнаю верхняю мяжою. Разгледзім яго ўласцівасці.
□ Няхай ![]() і
і
![]() . Тады
. Тады
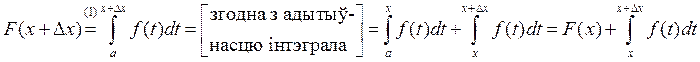 .
.
Адкуль 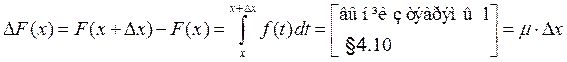 .
Гэта азначае, што
.
Гэта азначае, што ![]() , г. зн.
, г. зн. ![]() ёсць непарыўная на
ёсць непарыўная на ![]() . ■
. ■
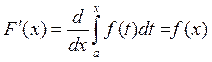 .
. □ Як і ў папярэдняй тэарэме ![]() ,
, ![]() ,
, 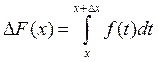 . Далей маем
. Далей маем
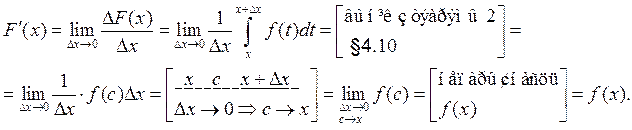
■
Вынік. Калі функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() , то на гэтым
адрэзку
, то на гэтым
адрэзку ![]() мае першаісную, якою
з’яўляецца
мае першаісную, якою
з’яўляецца 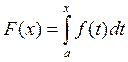 .
.
□ Сапраўды, ![]() .■
.■
1º. Формула Ньютана-Ляйбніца.
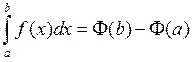 , якую
называюць формулаю Ньютана-Ляйбніца.
, якую
называюць формулаю Ньютана-Ляйбніца. □ Адпаведна выніку з тэарэмы Барроў адной з
першаісных для функцыі ![]() ёсць
ёсць 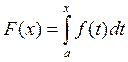 . З
формулы, якая падае агульны выгляд першаісных, вынікае
. З
формулы, якая падае агульны выгляд першаісных, вынікае 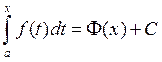 .
Беручы
.
Беручы ![]() , атрымаем
, атрымаем 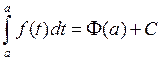 ,
адкуль
,
адкуль ![]() .
Такім чынам,
.
Такім чынам, 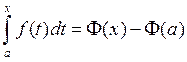 .
Гэтая роўнасць праўдзіцца
.
Гэтая роўнасць праўдзіцца ![]() , а таму пры
, а таму пры ![]() маем
маем 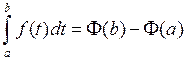 .
■
.
■
Заўвага 1. Формулу Ньютана-Ляйбніца
запісваюць таксама ў выглядзе 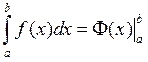 .
.
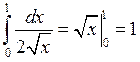 . Ці правільна? Не, функцыя
. Ці правільна? Не, функцыя 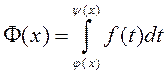 дакажыце праўдзівасць
формулы
дакажыце праўдзівасць
формулы 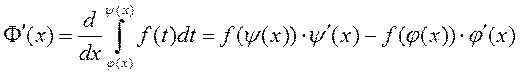 , калі
, калі 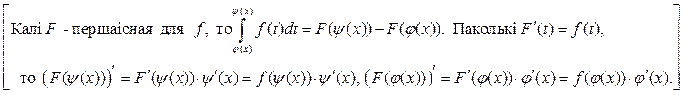
Пакажам на прыкладах, як вызначаны інтэграл можна скарыстаць пры вылічэнні некаторых лімітаў.
►Абазначым
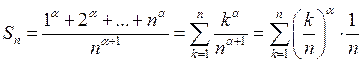 . Выраз
. Выраз ![]() можна разглядаць як
інтэгральную суму для функцыі
можна разглядаць як
інтэгральную суму для функцыі ![]() на адрэзку
на адрэзку ![]() з падзелам
з падзелам ![]() і выбаркаю
і выбаркаю ![]() . Пры гэтым
. Пры гэтым ![]() , а таму
, а таму
![]() ,
калі
,
калі ![]() . Паколькі
. Паколькі ![]() –
непарыўная на
–
непарыўная на ![]() , то
, то 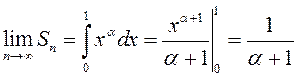 ◄
◄
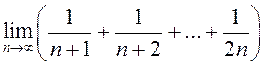 .
. ►Выраз 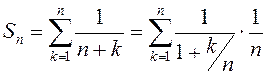 – інтэгральная сума для
функцыі
– інтэгральная сума для
функцыі ![]() на адрэзку
на адрэзку ![]() , а таму
, а таму 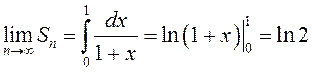 . ◄
. ◄
2º. Замена зменнай .
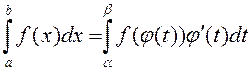 ,
(1)
,
(1)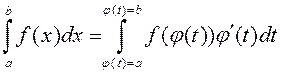 .
. □ Калі ![]() –
першаісная для функцыі
–
першаісная для функцыі ![]() , г. зн.
, г. зн. ![]() , то, згодна з формулаю
Ньютана-Ляйбніца,
, то, згодна з формулаю
Ньютана-Ляйбніца,
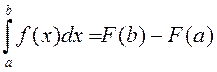 .
(2)
.
(2)
Паколькі ![]() , то
функцыя
, то
функцыя ![]() ёсць першаісная для функцыі
ёсць першаісная для функцыі
![]() . Карыстаючыся Формулаю
Ньютана-Ляйбніца і ўлічваючы ўмову
. Карыстаючыся Формулаю
Ньютана-Ляйбніца і ўлічваючы ўмову ![]() , атрымаем
, атрымаем
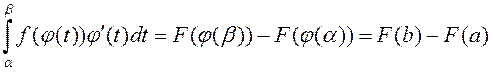 .
(3)
.
(3)
З роўнасцяў (2) і (3) вынікае (1). ■
Заўвага1. Калі формулаю (1) кіруюцца справа налева, то пішуць
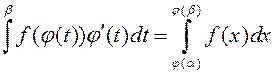
Заўвага2. Формула (1) праўдзівая і ў выпадку, калі ![]() ёсць толькі інтэгравальная,
але
ёсць толькі інтэгравальная,
але ![]() – не толькі непарыўная , але
не змяняе знаку на
– не толькі непарыўная , але
не змяняе знаку на ![]() , г. зн. –
манатонная.
, г. зн. –
манатонная.
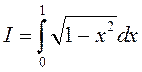 .
. ►1) 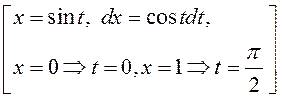
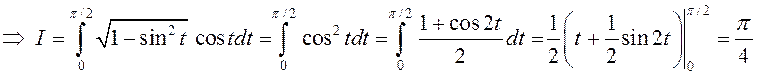 .
.
2) 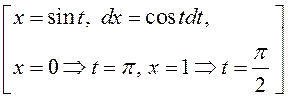
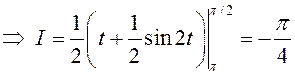 .
.
(Чаму? Бо ![]() , калі
, калі ![]() .)
.)
3) 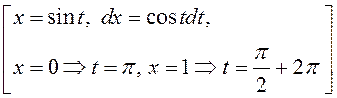
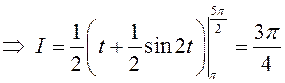 .
.
(Чаму? Тут ![]() .)
.)
4) 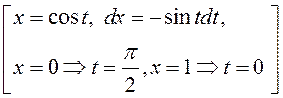
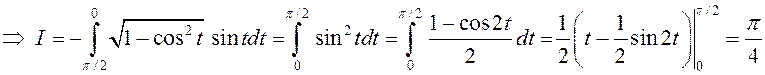 .
◄
.
◄
3º. Інтэграванне цотнай, няцотнай і перыядычнай функцый.
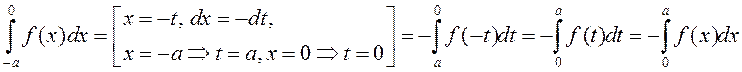 . Такім чынам,
. Такім чынам,
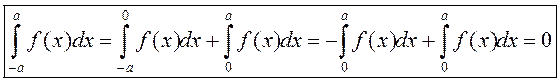 .
2) Калі ж
.
2) Калі ж 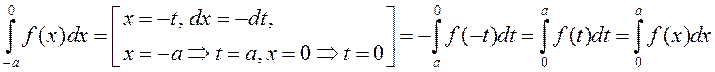 . Таму
. Таму
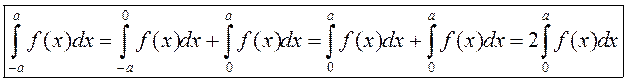 .
.  .
. Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.