► Першаісная функцыі ![]() ёсць
ёсць ![]() – абмежаваная, а функцыя
– абмежаваная, а функцыя ![]() – манатонная і бясконца
малая на прамежку
– манатонная і бясконца
малая на прамежку ![]() . Паводле прыкметы
Дырыхле інтэграл
. Паводле прыкметы
Дырыхле інтэграл 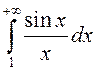 – збежны.
– збежны.
Даследуем інтэграл на абсалютную збежнасць. З
няроўнасці 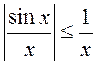 нічога не
вынікае. Але
нічога не
вынікае. Але 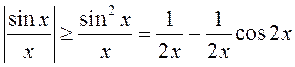 і пры гэтым
інтэграл
і пры гэтым
інтэграл 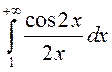 паводле прыкметы
Дырыхле ёсць збежны.
паводле прыкметы
Дырыхле ёсць збежны.
Калі б інтэграл 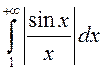 быў
збежны, то з няроўнасці
быў
збежны, то з няроўнасці 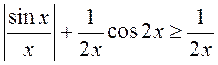 мелі
б, што
мелі
б, што ![]() – збежны, але ж ён
разбежны. Такім чынам,
– збежны, але ж ён
разбежны. Такім чынам, 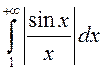 –
разбежны, а інтэграл
–
разбежны, а інтэграл 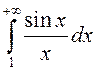 – умоўна
збежны. ◄
– умоўна
збежны. ◄
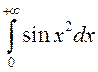 на
збежнасць.
на
збежнасць. ►Запішам падынтэгральную
функцыю у выглядзе ![]() . Паколькі
першаісная
. Паколькі
першаісная ![]() – абмежаваная, а функцыя
– абмежаваная, а функцыя ![]() манатонна імкнецца да нуля,
то на падставе прыкметы Дырыхле інтэграл Фрэнэля – збежны.
манатонна імкнецца да нуля,
то на падставе прыкметы Дырыхле інтэграл Фрэнэля – збежны.
Зазначым, што інтэграл 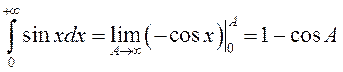 – разбежны. ◄
– разбежны. ◄
def. Калі функцыя ![]() ёсць неабмежаваная ў пункце
ёсць неабмежаваная ў пункце ![]() , і інтэгравальная на кожным
адрэзку
, і інтэгравальная на кожным
адрэзку ![]() ( упрыватнасці
( упрыватнасці ![]() ёсць абмежаваная на адрэзку
ёсць абмежаваная на адрэзку ![]() ), то пункт
), то пункт ![]() называюць
асаблівым пунктам функцыі
называюць
асаблівым пунктам функцыі ![]() .
.
def. Ліміт
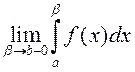 (1)
(1)
называюць неўласцівым
інтэгралам ад неабмежаванай функцыі на адрэзку ![]() (або неўласцівым інтэгралам другога роду,
НІ-2) і абазначаюць
(або неўласцівым інтэгралам другога роду,
НІ-2) і абазначаюць
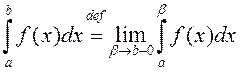 .
(2)
.
(2)
Калі існуе канечны ліміт (1), то Ні-2 (2) называюць збежным. Калі ж ліміт (1) не існуе, то кажуць, што інтэграл (2) ёсць разбежны.
Заўвага 1. Калі ![]() , то інтэгралы
, то інтэгралы 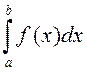 і
і 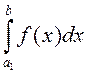 збягаюцца або разбягаюцца
адначасова.
збягаюцца або разбягаюцца
адначасова.
Заўвага 2. Формулу (2) бывае больш зручна запісваць у выглядзе
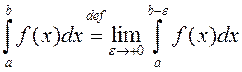 .
(3)
.
(3)
Аналагічна азначаецца
неўласцівы інтэграл 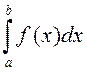 , калі
, калі ![]() ёсць асаблівы пункт функцыі
ёсць асаблівы пункт функцыі
![]()
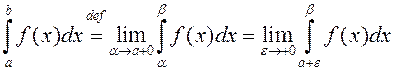 .
.
Калі ж пункт ![]() ёсць асаблівы пункт функцыі
ёсць асаблівы пункт функцыі
![]() , і інтэгралы
, і інтэгралы 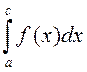 і
і
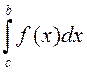 – збежныя, то
– збежныя, то
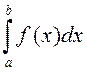 =
=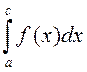 +
+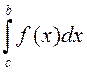 .
.
Далей для пэўнасці мы будзем вывучаць НІ-2, якія азначаюцца формуламі (2), або (3).
Паміж НІ-1 і НІ-2 існуе пэўная сувязь.
Сапраўды, няхай ![]() ёсць інтэгравальная на
ёсць інтэгравальная на ![]() і
і ![]() – яе асаблівы пункт. У
інтэграле з (3)
– яе асаблівы пункт. У
інтэграле з (3) 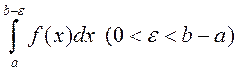 зробім замену
зробім замену
![]()
і атрымаем 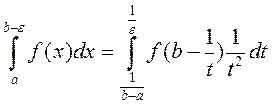 . Такім чынам, прыходзім да
роўнасці
. Такім чынам, прыходзім да
роўнасці
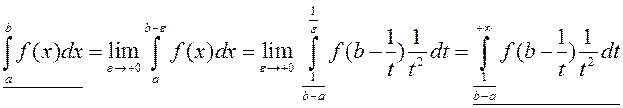 .
.
Гэта азначае, што для НІ-2
праўдзяцца ўласцівасці, аналагічныя адпаведным уласцівасцям для НІ-1, а на
збежнасць НІ–2 можна даследаваць як НІ–1, які атрымліваецца з яго пасля замены ![]() .
.
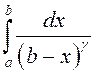 .
.► Калі ў гэтым інтэграле зрабіць вышэй згаданую замену
![]() , то мы прыходзім да інтэграла
, то мы прыходзім да інтэграла 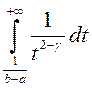 , які ёсць збежны толькі пры
, які ёсць збежны толькі пры
![]() або
або ![]() . Такім чынам, разгляданы
намі інтэграл ёсць збежны пры
. Такім чынам, разгляданы
намі інтэграл ёсць збежны пры ![]() і
разбежны пры
і
разбежны пры ![]() . У прыватнасці,
. У прыватнасці, ![]() ёсць збежны толькі пры
ёсць збежны толькі пры ![]() . ◄
. ◄
Аналагічна, як і для НІ-1 можна даказаць наступныя тэарэмы.
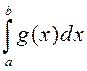 ёсць збежны, то
ёсць збежны, то 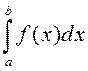 таксама збежны. Калі ж
таксама збежны. Калі ж 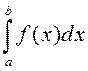 разбежны, то
разбежны, то 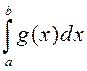 .
.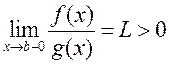 то абодва інтэгралы
то абодва інтэгралы 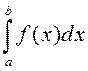 і
і 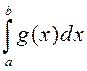 збягаюцца або разбягаюцца адначасова. У прыватнасці гэта мае месца,
калі
збягаюцца або разбягаюцца адначасова. У прыватнасці гэта мае месца,
калі Вынік Калі 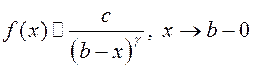 , то
, то 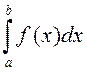 збежны толькі пры
збежны толькі пры ![]() .
.
► Паколькі ![]() , то
, то ![]() , а таму
, а таму ![]() . Такім чынам, інтэграл
. Такім чынам, інтэграл ![]() разбежны, паколькі
разбежны, паколькі ![]() . ◄
. ◄
def. НІ-2 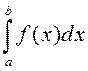 называецца абсалютна
збежным, калі збягаецца інтэграл
называецца абсалютна
збежным, калі збягаецца інтэграл 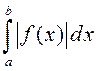 .
З абсалютнай збежнасці інтэграла вынікае яго збежнасць.
.
З абсалютнай збежнасці інтэграла вынікае яго збежнасць.
def. Калі НІ-2 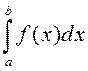 ёсць збежны, а інтэграл
ёсць збежны, а інтэграл
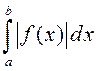 – разбежны то НІ-2
называецца ўмоўна збежным.
– разбежны то НІ-2
называецца ўмоўна збежным.
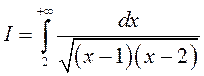 .
. ► Паколькі 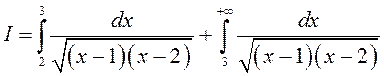 , то пабудуем для
падынтэгральнай функцыі эквівалентныя у пунктах
, то пабудуем для
падынтэгральнай функцыі эквівалентныя у пунктах ![]() і
і
![]() :
:
1).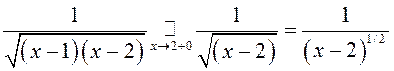 – інтэграл збежны;
– інтэграл збежны;
2).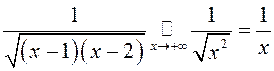 – інтэграл разбежны.
– інтэграл разбежны.
Такім чынам, інтэграл ![]() ёсць разбежны. ◄
ёсць разбежны. ◄
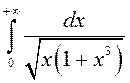 .
. ► Паколькі 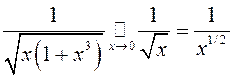 , то ў пункце
, то ў пункце ![]() інтэграл збежны, а паколькі
інтэграл збежны, а паколькі
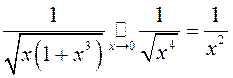 , то і ў пункце
, то і ў пункце ![]() інтэграл збежны. Такім
чынам, інтэграл збежны. ◄
інтэграл збежны. Такім
чынам, інтэграл збежны. ◄
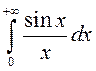 .
. ► Паколькі 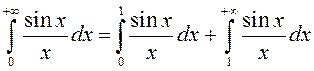 , то першы інтэграл
існуе як вызначаны, а другі ёсць збежны паводле прыкметы Дырыхле. Такім чынам,
інтэграл збежны.◄
, то першы інтэграл
існуе як вызначаны, а другі ёсць збежны паводле прыкметы Дырыхле. Такім чынам,
інтэграл збежны.◄
► Заўсёды разбежны. ◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.