З улікам (2) атрымаем 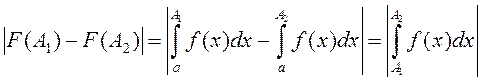 .
.
Такім чынам, мы атрымалі
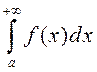 быў збежным, неабходна і дастаткова, каб
быў збежным, неабходна і дастаткова, каб 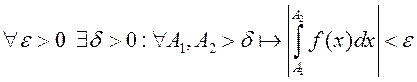 .
.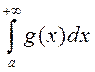 ёсць збежны, то
ёсць збежны, то 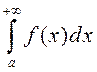 таксама збежны.
таксама збежны. □ Паколькі 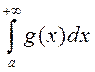 ёсць збежны, то для яго мае месца крытэр Кашы
ёсць збежны, то для яго мае месца крытэр Кашы
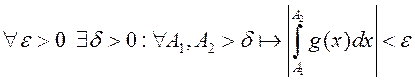 .
.
Калі ![]() , то
, то 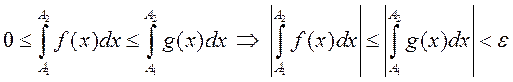 . Калі ж
. Калі ж ![]() , то
, то 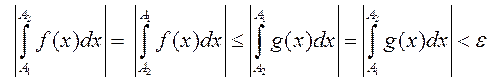 . Такім чынам, для функцыі
. Такім чынам, для функцыі ![]() выконваюцца ўмовы крытэра
Кашы, а таму
выконваюцца ўмовы крытэра
Кашы, а таму 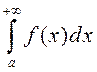 – збежны. ■
– збежны. ■
Вынік. (дастатковая ўмова
разбежнасці) Калі ![]() і
і 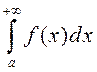 ёсць
разбежны, то
ёсць
разбежны, то 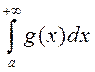 таксама
разбежны.
таксама
разбежны.
□ Сапраўды, калі дапусціць адваротнае,
г. зн. інтэграл 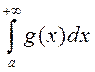 – збежны, то на падставе тэарэмы 1
– збежны, то на падставе тэарэмы 1 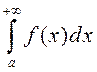 павінен
быць збежным ?!? ■
павінен
быць збежным ?!? ■
Заўвага 1. Калі
няроўнасць ![]() выконваецца толькі
выконваецца толькі ![]()
![]() ,
то тэарэма 1 таксама праўдзівая.
,
то тэарэма 1 таксама праўдзівая.
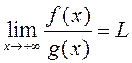 . Тады:
. Тады: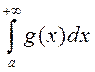 ёсць збежны і
ёсць збежны і 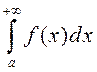 – таксама збежны;
– таксама збежны;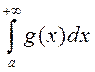 ёсць разбежны і
ёсць разбежны і 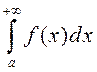 – разбежны.
– разбежны. □ 1). Паколькі ![]() – ліміт функцыі
– ліміт функцыі ![]() , то
, то 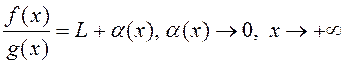 . Паколькі
. Паколькі ![]() – абмежаваная, то
– абмежаваная, то ![]() . Гэта значыць, што
. Гэта значыць, што 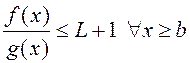 . Паколькі
. Паколькі ![]() , то
, то ![]() . З тэарэмы 1 і
заўвагі 1 вынікае праўдзівасць сцверджання 1).
. З тэарэмы 1 і
заўвагі 1 вынікае праўдзівасць сцверджання 1).
2). Калі ![]() , то
, то 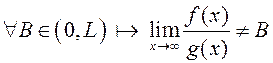 , а гэта азначае, што
, а гэта азначае, што
(гэта ёсць адмаўленне для 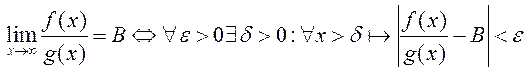 )
)
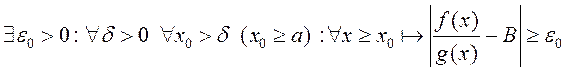 .
.
З апошняй няроўнасці атрымліваем 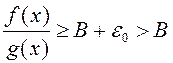 . Такім чынам,
. Такім чынам, ![]() . Паколькі
. Паколькі 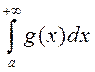 – разбежны, то
– разбежны, то 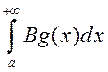 таксама
разбежны (
таксама
разбежны (![]() ), бо інакш
), бо інакш 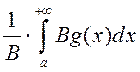 – збежны. На падставе выніка з тэарэмы 1 атрымліваем
праўдзівасць сцверджання 2). ■
– збежны. На падставе выніка з тэарэмы 1 атрымліваем
праўдзівасць сцверджання 2). ■
Заўвага 2. Калі ![]() ,г.зн.
,г.зн.
![]() і
і ![]() – функцыі аднаго парадку,
то абодва інтэгралы або збежныя, або разбежныя адначасова.
– функцыі аднаго парадку,
то абодва інтэгралы або збежныя, або разбежныя адначасова.
Вынік 1. Калі ![]() і
і ![]() , то
, то 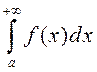 і
і 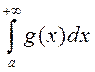 збежныя або разбежныя адначасова.
збежныя або разбежныя адначасова.
Вынік 2. Калі ![]() , то
, то 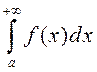 збежны
пры
збежны
пры ![]() і разбежны пры
і разбежны пры ![]() .
.
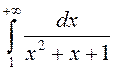 збежны, бо
збежны, бо б) 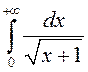 разбежны, бо
разбежны, бо 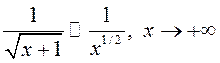 .
.
в) 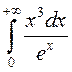 збежны, бо
збежны, бо ![]() нарастае хутчэй за любую
ступень, таму
нарастае хутчэй за любую
ступень, таму ![]() . Такім чынам,
. Такім чынам, 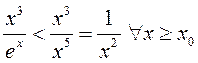
Практыкаванне. Дакажыце, што 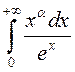 збежны пры
збежны пры ![]() .
.
г) 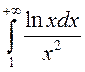 збежны, бо
збежны, бо ![]() – лянівая функцыя, таму
– лянівая функцыя, таму ![]() . Такім чынам,
. Такім чынам, 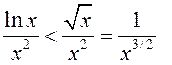 .
.
Практыкаванне. Дакажыце, што 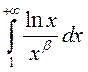 збежны
пры
збежны
пры ![]() .
.
def. Неўласцівы інтэграл 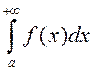 называецца
абсалютна збежным, калі ін-тэграл
называецца
абсалютна збежным, калі ін-тэграл 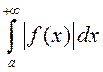 ёсць
збежны.
ёсць
збежны.
Заўвага 3. З абсалютнай збежнасці
НІ-1 вынікае яго збежнасць, паколькі 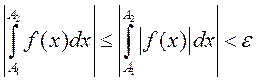 ,
г. зн. выконваецца крытэр Кашы.
,
г. зн. выконваецца крытэр Кашы.
Заўвага 4. Калі 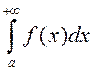 ёсць
абсалютна збежны, а функцыя
ёсць
абсалютна збежны, а функцыя ![]() –
абмежаваная на
–
абмежаваная на ![]() , то
, то 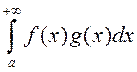 – абсалютна збежны.
– абсалютна збежны.
Сапраўды, ![]() .
Тады
.
Тады ![]() , а паколькі
, а паколькі 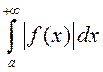 – збежны, то на падставе
прыкметы параўнання
– збежны, то на падставе
прыкметы параўнання 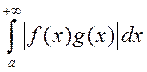 .
.
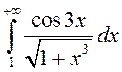 ёсць абсалютна збежны,
паколькі
ёсць абсалютна збежны,
паколькі 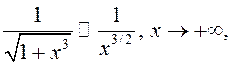 і інтэграл
і інтэграл 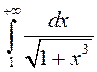 абсалютна збежны.
абсалютна збежны.Пры даследаванні неўласцівых інтэгралаў на абсалютную збежнасць выкарыстоўваюць тэарэмы 1 і 2 і вынікі з гэтых тэарэм.
def. Калі інтэграл 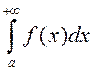 ёсць збежны, а
ёсць збежны, а 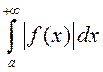 – разбежны, то інтэграл
– разбежны, то інтэграл 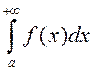 называецца ўмоўна
збежным.
называецца ўмоўна
збежным.
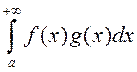 – збежны.
– збежны. □ Пераканаемся, што для функцыі ![]() выконваецца
крытэр інтэгра-вальнасці Кашы. Правядзем інтэграванне часткамі
выконваецца
крытэр інтэгра-вальнасці Кашы. Правядзем інтэграванне часткамі
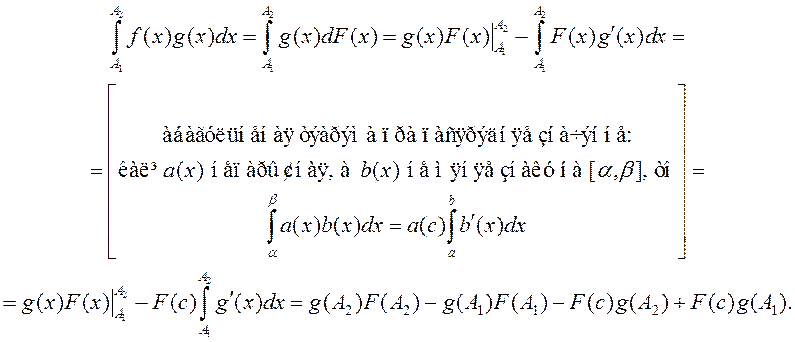
Паколькі ![]() абмежаваная,
то
абмежаваная,
то ![]() . Такім чынам, маем
. Такім чынам, маем
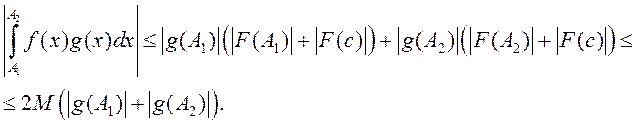
Паколькі ![]() , то
, то ![]() . Таму
. Таму
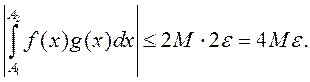
Згодна з крытэрам Кашы інтэграл 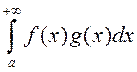 –
збежны. ■
–
збежны. ■
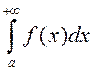 – збежны, а функцыя
– збежны, а функцыя 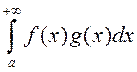 – збежны.
– збежны. □ Доказ вынікае з прыкметы Дырыхле. Паколькі
вытворная функцыі ![]() не
мяняе знаку, то яна манатонная на
не
мяняе знаку, то яна манатонная на ![]() ,
а тады з яе абмежаванасці вынікае існаванне ліміта
,
а тады з яе абмежаванасці вынікае існаванне ліміта ![]() . З роўнасці
. З роўнасці
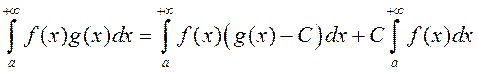
вынікае: дастаткова даказаць збежнасць 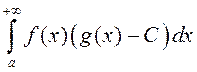 .
.
Паколькі ![]() і функцыя
і функцыя ![]() –
манатонная, то, каб скарыстацца прыкметаю Дырыхле, дастаткова даказаць,
што першаісная для
–
манатонная, то, каб скарыстацца прыкметаю Дырыхле, дастаткова даказаць,
што першаісная для ![]() ёсць абмежаваная.
ёсць абмежаваная.
Сапраўды, паколькі інтэграл 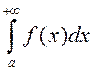 –
збежны, то існуе ліміт
–
збежны, то існуе ліміт 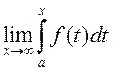 , а
інтэграл
, а
інтэграл 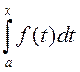 – першаісная для непарыўнай
функцыі
– першаісная для непарыўнай
функцыі ![]() ёсць функцыя непарыўная на любым адрэзку
ёсць функцыя непарыўная на любым адрэзку ![]() . Паколькі ліміт гэтай
функцыі існуе на
. Паколькі ліміт гэтай
функцыі існуе на ![]() , то яна –
абмежаваная на
, то яна –
абмежаваная на ![]() . ■
. ■
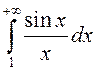 .
. Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.