3) у
інтэгралах ад функцый ![]() вылічэнне
інтэграла зводзіцца да раўнання ў дачыненні да зыходнага інтэграла.
вылічэнне
інтэграла зводзіцца да раўнання ў дачыненні да зыходнага інтэграла.
► 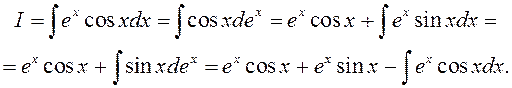
Прышлі да раўнання ![]() ◄
◄
Прыклад8.![]() (гл.
Прыклад 3)
(гл.
Прыклад 3)
►
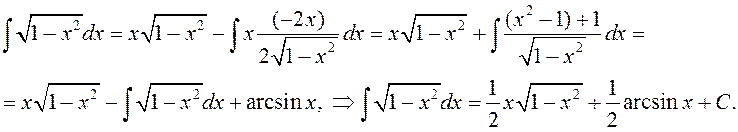
◄
Няхай ![]() –
рацыянальная функцыя, дзе
–
рацыянальная функцыя, дзе ![]() мнагасклады
супеняў
мнагасклады
супеняў ![]() і
і ![]() . Калі
. Калі ![]() (г. зн. рацыянальная
функцыя ёсць няправільная), то згодна з тэарэмаю пра выяўленне мнагаскладу
(г. зн. рацыянальная
функцыя ёсць няправільная), то згодна з тэарэмаю пра выяўленне мнагаскладу ![]() . Такім чынам, маем
. Такім чынам, маем 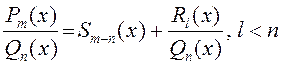 , г. зн. рацынальную
функцыю можна падаць як суму мнагаскладу і правільнай рацыянальнай функцыі.
Мнагасклад інтэгруецца як сума ступеневых функцый. Што да правільнай
рацыянальнай функцыі, то згодна з тэарэмаю пра раскладанне правільнай
рацыянальнай функцыі на суму простых дробаў, нам дастаткова навучыцца
інтэграваць простыя дробы:
, г. зн. рацынальную
функцыю можна падаць як суму мнагаскладу і правільнай рацыянальнай функцыі.
Мнагасклад інтэгруецца як сума ступеневых функцый. Што да правільнай
рацыянальнай функцыі, то згодна з тэарэмаю пра раскладанне правільнай
рацыянальнай функцыі на суму простых дробаў, нам дастаткова навучыцца
інтэграваць простыя дробы:
1) 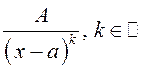 ; 2)
; 2) 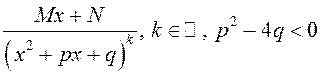 .
.
1а) (![]() ).
). ![]() .
.
2а) (![]() ).
). 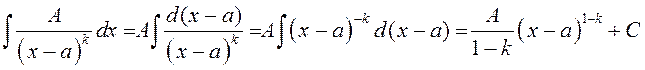 .
.
2а) (![]() ).
).
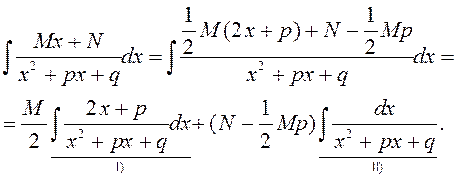
![]() .
. 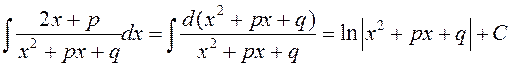 .
.
![]() .
. 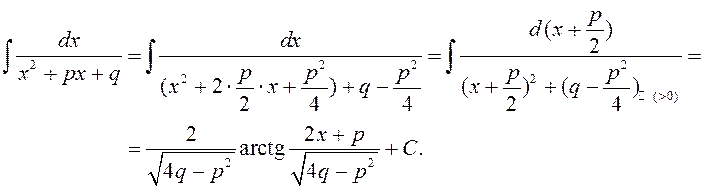
2б) ![]() .
.
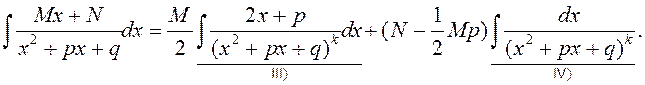
![]()
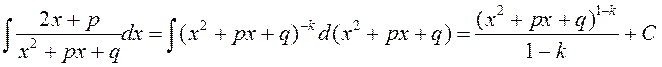 .
.
![]()
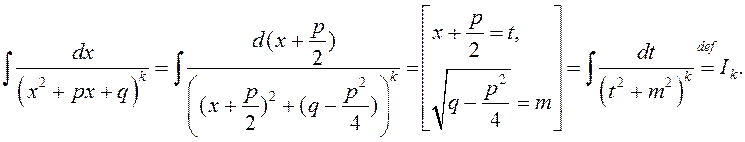
Зоймемся вылічэннем апошняга інтэграла.
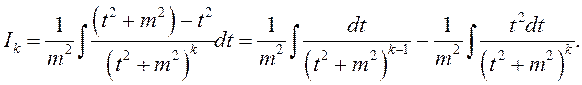 (1)
(1)
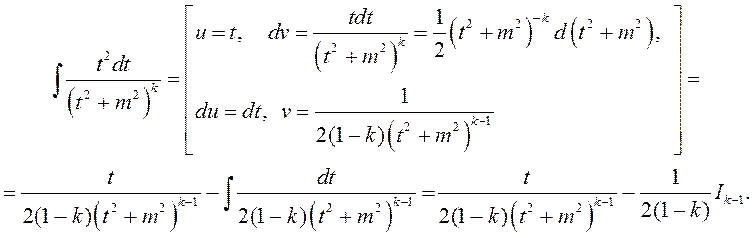 (2)
(2)
Падставім (2) у (1)
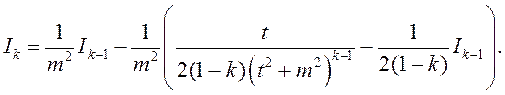
Адкуль атрымліваем
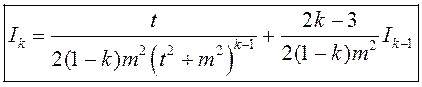 (3)
(3)
– рэкурэнтную формулу для вылічэння інтэграла 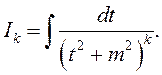
Прыклад 1. Вылічыць 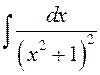 .
.
► 1) (Паводле формулы (3))
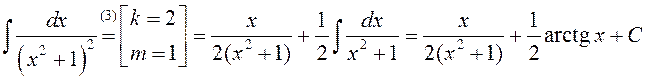 .
.
2) (Паводле метада) 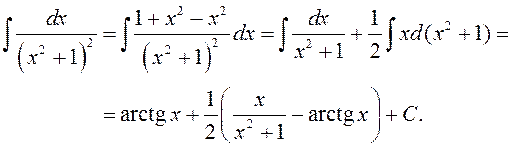 ◄
◄
Прыклад 2. Вылічыць 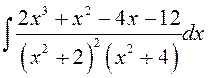 .
.
► метадам нявызначаных каэфіцыентаў раскладзем падынтэгральную функцыю на суму простых дробаў
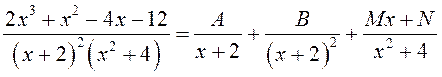 .
.
Спосабам дамнажэння вылічаем канстанты ![]() :
:
![]() ,
,
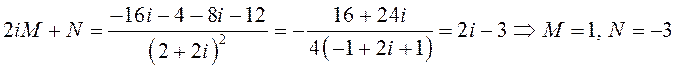 .
.
Пры ![]() маем
маем ![]() . Такім чынам,
. Такім чынам, 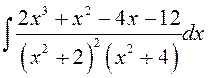 =
=
=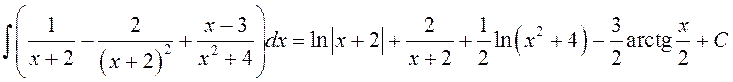 . ◄
. ◄
Заўвага. Калі назоўнік ![]() правільнай рацыянальнай
функцыі
правільнай рацыянальнай
функцыі ![]() мае кратныя корні, то пры
вылічэнні інтэграла карыстаюцца метадам Астраградскага, паводле якога інтэграл
шукаецца ў выглядзе
мае кратныя корні, то пры
вылічэнні інтэграла карыстаюцца метадам Астраградскага, паводле якога інтэграл
шукаецца ў выглядзе
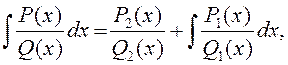 (4)
(4)
дзе ![]() –
мнагасклад, які мае тыя ж корні, што і мнагасклад
–
мнагасклад, які мае тыя ж корні, што і мнагасклад ![]() ,
але кратрасці 1, а
,
але кратрасці 1, а 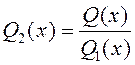 . Пры гэтым
функцыі
. Пры гэтым
функцыі 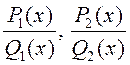 – правільныя рацыянальныя
функцыі з нявызначанымі ў лічніку каэфіцыентамі.
– правільныя рацыянальныя
функцыі з нявызначанымі ў лічніку каэфіцыентамі.
Каэфіцыенты мнагаскладаў ![]() вылічаюцца метадам
адпаведных каэфіцыентаў з роўнасці, якая атрымліваецца пасля дыферэнцавання
(4).
вылічаюцца метадам
адпаведных каэфіцыентаў з роўнасці, якая атрымліваецца пасля дыферэнцавання
(4).
Прыклад 3. Вылічыць 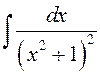 .
.
► Згодна з метадам Астраградскага запішам роўнасць
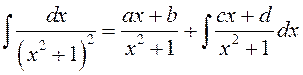 , пасля
дыферэнцавання якой маем
, пасля
дыферэнцавання якой маем
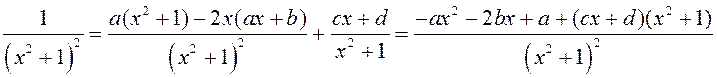 .
.
З апошняй роўнасці метадам адпаведных каэфіцыентаў атрымліваем сістэму
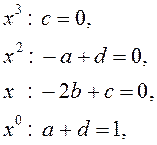
адкуль ![]() Такім
чынам,
Такім
чынам, 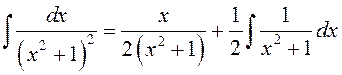 .
.
Канчаткова маем 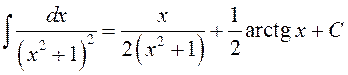 .
◄
.
◄
def
Мнагаскладам ступені ![]() ад дзвюх зменных
ад дзвюх зменных ![]() і
і ![]() называецца выраз
называецца выраз
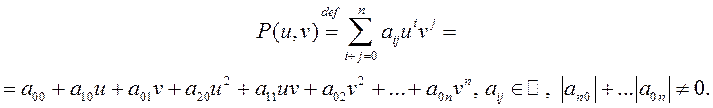
Рацыянальнай функцыяй дзвюх зменных называецца выраз 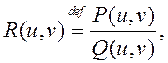 дзе
дзе ![]() – мнагасклады.
– мнагасклады.
Зазначым пры гэтым, што складаная функцыя ![]() , дзе
, дзе ![]() – рацыянальныя функцыі,
ёсць таксама рацыянальная функцыя.
– рацыянальныя функцыі,
ёсць таксама рацыянальная функцыя.
1º. Інтэграванне дробава-лінейнай ірацыянальнасці.
Будзем разглядаць інтэгралы тыпу
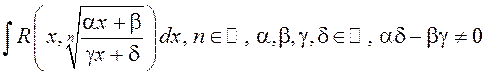 ,
г. зн.
,
г. зн. 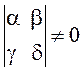 .
.
Зробім замену зменнай
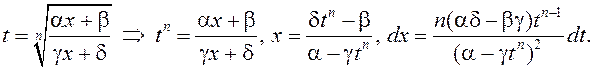
Маем
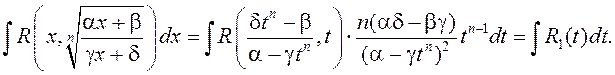
Прыклад 1. Вылічыць 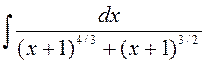 .
.
► Спачатку зробім наступнае пераўтварэнне падынтэгральнай функцыі
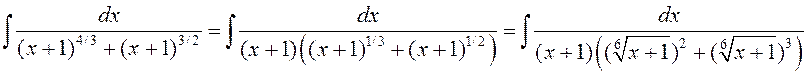 .
.
Пасля гэтага зробім замену ![]() . Маем
. Маем
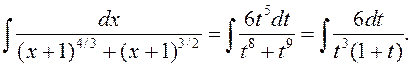
Падынтэгральную функцыю раскладзем на суму простых дробаў
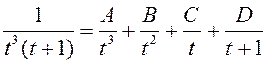 .
.
Метадам дамнажэння вылічаем ![]() .
Надаючы прыватныя значэнні
.
Надаючы прыватныя значэнні ![]() і
і ![]() , атрымаем
, атрымаем ![]() ,
, ![]() . Адкуль
. Адкуль ![]()
Маем 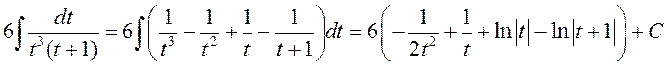 .
.
Такім чынам, 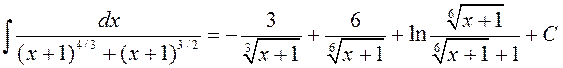 .
◄
.
◄
2º. Інтэграванне рацыянальна-трыганаметрычных функцый.
Інтэгралы тыпу ![]() заўсёды
рацыяналізуюцца універсальнай падстановай
заўсёды
рацыяналізуюцца універсальнай падстановай ![]() . Сапраўды
. Сапраўды
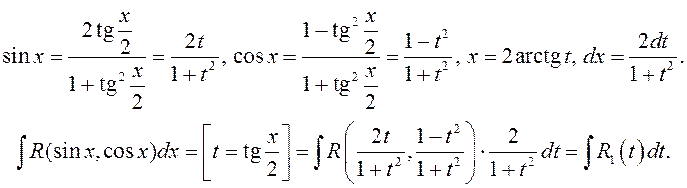
У некаторых прыватных выпадках вылічэнне інтэгралаў ад рацыянальна-трыганаметрычных функцый праводзіцца пры дапамозе больш зручных падстановаў.
а) Калі ![]() ,
то інтэграл рацыяналізуецца падста-новаю
,
то інтэграл рацыяналізуецца падста-новаю ![]()
б) Калі ![]() , то інтэграл
рацыяналізуецца падста-новаю
, то інтэграл
рацыяналізуецца падста-новаю ![]()
б) Калі ![]() , то інтэграл
рацыяналізуецца падста-новаю
, то інтэграл
рацыяналізуецца падста-новаю ![]()
Прыклад 2. 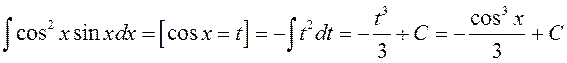
Прыклад 3.
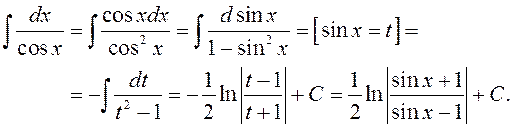
Прыклад 4.
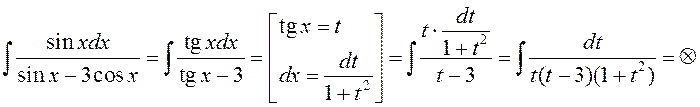 .
.
Падынтэгральную функцыю раскладзем на суму простых дробаў з нявызнача-нымі
каэфіцыентамі 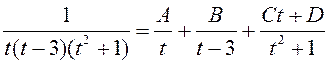 і метадам
дамнажэння атрымаем
і метадам
дамнажэння атрымаем 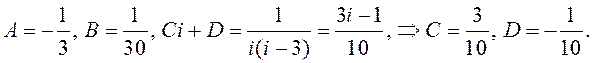
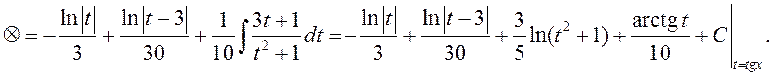
3º. Квадратовыя ірацыянальнасці.
Будзем разглядаць інтэгралы тыпу ![]()
1) Калі ![]() , то
, то ![]() , г. зн. што
падінтэгральная функцыя ёсць рацыянальная функцыя .
, г. зн. што
падінтэгральная функцыя ёсць рацыянальная функцыя .
2) Калі ![]() , то
, то 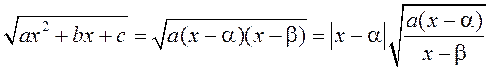 , г. зн.
падінтэгральная функцыя ёсць дробава-лінейная ірацыянальнасць.
, г. зн.
падінтэгральная функцыя ёсць дробава-лінейная ірацыянальнасць.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.