Паняцці ліміту і функцыі ёсць асноўныя паняцці матэматычнага аналізу. Пачатак вывучэння паняцця ліміту зроблены ў элементарнай матэматыцы, дзе пры дапамозе лімітавых пераходаў вызначаецца даўжыня акружыны, аб’ём цыліндра, конуса і інш. У гэтым раздзеле мы вывучым паняцці ліміту паслядоўнасці, ліміту функцыі і непарыўнасць функцыі.
def: Калі кожнаму натуральнаму ліку ![]() ставіцца ў адпаведнасць
рэчаісны лік
ставіцца ў адпаведнасць
рэчаісны лік ![]() , то такую функцыю называюць
лікавай паслядоўнасцю і абазначаюць
, то такую функцыю называюць
лікавай паслядоўнасцю і абазначаюць ![]() . Інакш кажучы, лікавая
паслядоўнасць ёсць занумараванае бясконцае мноства рэчаісных лікаў
. Інакш кажучы, лікавая
паслядоўнасць ёсць занумараванае бясконцае мноства рэчаісных лікаў ![]() =
=![]() .
Лікі
.
Лікі ![]() называюцца элементамі
лікавай паслядоўнасці
называюцца элементамі
лікавай паслядоўнасці ![]() ,
сымбаль
,
сымбаль ![]() называецца агульным
элементам лікавай паслядоўнасці, а індэкс
называецца агульным
элементам лікавай паслядоўнасці, а індэкс ![]() –
яго нумарам. Такім чынам, кожная лікавая паслядоўнасць змяшчае
бясконца многа элементаў, але мноства яе значэнняў можа складацца і з канечнай
колькасці лікаў.
–
яго нумарам. Такім чынам, кожная лікавая паслядоўнасць змяшчае
бясконца многа элементаў, але мноства яе значэнняў можа складацца і з канечнай
колькасці лікаў.
Прыклады. 1) Калі лікавая паслядоўнасць
![]() мае агульны элемент
мае агульны элемент ![]() , г.зн.
, г.зн. 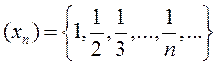 , то мноства яе значэнняў
ёсць бясконцае і складаецца з рацыянальных лікаў тыпу
, то мноства яе значэнняў
ёсць бясконцае і складаецца з рацыянальных лікаў тыпу ![]() .
.
2) У паслядоўнасці ![]() , г.зн.
, г.зн. ![]() мноства значэнняў
складаецца з двух лікаў : 0 і 2.
мноства значэнняў
складаецца з двух лікаў : 0 і 2.
3) Лікавая паслядоўнасць ![]() называецца
сталаю паслядоўнасцю і мноства яе значэнняў складаецца з адзінага
рэчаіснага ліку
называецца
сталаю паслядоўнасцю і мноства яе значэнняў складаецца з адзінага
рэчаіснага ліку ![]() .
.
Увядзем арыфметычныя дзеянні над лікавымі паслядоўнасцямі.
def: Няхай зададзены дзве лікавыя паслядоўнасці ![]() . Сумай лікавых
паслядоўнасцяў
. Сумай лікавых
паслядоўнасцяў ![]() і
і ![]() называецца лікавая
паслядоўнасць
называецца лікавая
паслядоўнасць ![]() ; розніцаю
–
; розніцаю
– ![]() ; здабыткам
–
; здабыткам
– ![]() ; дзеллю –
; дзеллю – ![]() , калі
, калі ![]() ; здабыткам лікавай
паслядоўнасці
; здабыткам лікавай
паслядоўнасці ![]() на лік
на лік ![]() называецца лікавая
паслядоўнасць
называецца лікавая
паслядоўнасць ![]() . Такім чынам,
. Такім чынам,
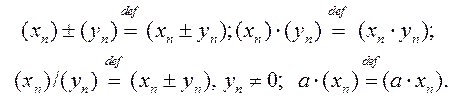
def: Лікавая паслядоўнасць ![]() называецца абмежаванаю
зверху [знізу], калі мноства яе элементаў
абмежаванае зверху [знізу], г.зн
называецца абмежаванаю
зверху [знізу], калі мноства яе элементаў
абмежаванае зверху [знізу], г.зн ![]() [
[![]() ]:
]: ![]() . Калі
лікавая паслядоўнасць абмежаваная як зверху, так і знізу, то яна называецца абмежаванаю
, г.зн.
. Калі
лікавая паслядоўнасць абмежаваная як зверху, так і знізу, то яна называецца абмежаванаю
, г.зн. ![]() . (Ці вынікае з умовы
. (Ці вынікае з умовы ![]() абмежаванасць паслядоўнасці
абмежаванасць паслядоўнасці
![]() ? Не, яна можа быць
неабмежаванаю знізу.)
? Не, яна можа быць
неабмежаванаю знізу.)
Практыкаванне Сфармуляваць азначэнне неабмежаванасці
лікавай паслядоўнасці ![]() . (
. (![]() )
)
Прыклады.
1) Лікавая паслядоўнасць ![]() –
абмежаваная знізу, але неабмежаваная зверху (1–
ніжняя мяжа) . Такім чынам, лікавая паслядоўнасць
–
абмежаваная знізу, але неабмежаваная зверху (1–
ніжняя мяжа) . Такім чынам, лікавая паслядоўнасць ![]() – неабмежаваная.
– неабмежаваная.
2) Лікавая паслядоўнасць ![]() –
абмежаваная. (0,1 – адпаведна ніжняя і верхняя
межы)
–
абмежаваная. (0,1 – адпаведна ніжняя і верхняя
межы)
3) Лікавая паслядоўнасць ![]() – неабмежаваная,
прычым з абодвух бакоў. (Чаму?)
– неабмежаваная,
прычым з абодвух бакоў. (Чаму?)
def: Лікавая паслядоўнасць ![]() называецца бясконца
вялікаю паслядоўнасцю (бвп), калі
называецца бясконца
вялікаю паслядоўнасцю (бвп), калі ![]() .
Гэтае азначэнне раўназначнае таму, што ў (бвп) толькі канечная
колькасць элементаў належыць адрэзку
.
Гэтае азначэнне раўназначнае таму, што ў (бвп) толькі канечная
колькасць элементаў належыць адрэзку ![]() .
.
Чым адрозніваецца бясконца вялікая паслядоўнасць ад неабмежаванай лікавай паслядоўнасці?
Заўвага. Усякая бясконца вялікая паслядоўнасць ёсць неабмежаваная,
але неабмежаваная лікавая паслядоўнасць можа і не быць бясконца вялікаю
паслядоўнасцю. Напрыклад, неабмежаваная лікавая паслядоўнасць ![]() не ёсць бясконца вялікая
паслядоўнасць таму, што пры
не ёсць бясконца вялікая
паслядоўнасць таму, што пры ![]() няроўнасць
няроўнасць
![]() не праўдзіцца для ўсіх
элементаў паслядоўнасці з няцотнымі нумарамі.
не праўдзіцца для ўсіх
элементаў паслядоўнасці з няцотнымі нумарамі.
def: Лікавая паслядоўнасць ![]() называецца
бясконца малою паслядоўнасцю (бмп), калі
называецца
бясконца малою паслядоўнасцю (бмп), калі ![]() . Гэтае азначэнне
раўназначнае таму, што ў (бмп) толькі канечная колькасць элементаў
належыць мноству
. Гэтае азначэнне
раўназначнае таму, што ў (бмп) толькі канечная колькасць элементаў
належыць мноству ![]() , або знаходзіцца
па-за інтэрвалам
, або знаходзіцца
па-за інтэрвалам ![]() .
.
Прыклад. Дакажам, што лікавая паслядоўнасць ![]() ёсць бясконца малая
паслядоўнасць.
ёсць бясконца малая
паслядоўнасць.
∆ Возьмем ![]() . З
няроўнасці
. З
няроўнасці ![]()
![]()
![]() . Калі
. Калі ![]() , то
, то ![]() , г.зн.
, г.зн. ![]() ёсць бясконца малая
паслядоўнасць. ◄
ёсць бясконца малая
паслядоўнасць. ◄
![]() Тэарэма (сувязь паміж (бмп) і (бвп)). Калі
лікавая паслядоўнасць
Тэарэма (сувязь паміж (бмп) і (бвп)). Калі
лікавая паслядоўнасць ![]() ёсць (бвп) і
ёсць (бвп) і ![]() то лікавая паслядоўнасць
то лікавая паслядоўнасць ![]() ёсць (бмп). Калі лікавая
паслядоўнасць
ёсць (бмп). Калі лікавая
паслядоўнасць ![]() – (бмп) і
– (бмп) і ![]() то лікавая паслядоўнасць
то лікавая паслядоўнасць ![]() – (бвп).
– (бвп).
□ Няхай ![]() – (бвп).
Возьмем
– (бвп).
Возьмем ![]() і назавем
і назавем ![]() . На падставе азначэння
бясконца вялікай паслядоўнасці для гэтага
. На падставе азначэння
бясконца вялікай паслядоўнасці для гэтага ![]() .
Адсюль вынікае
.
Адсюль вынікае ![]() , г.зн.
, г.зн. ![]() – (бмп).
– (бмп).
Аналагічна даказваецца другая частка тэарэмы. ■
М-Лема для (бмп). Калі ![]() дзе
дзе ![]() не залежыць ні ад
не залежыць ні ад ![]() , ні ад
, ні ад ![]() ,
то лікавая паслядоўнасць
,
то лікавая паслядоўнасць ![]() ёсць (бмп).
ёсць (бмп).
□ Возьмем ![]() і
назавем
і
назавем ![]() . На падставе ўмовы лемы для
гэтага
. На падставе ўмовы лемы для
гэтага ![]() . Абазначым далей праз
. Абазначым далей праз ![]() значэнне
значэнне ![]() . Такім чынам, маем
. Такім чынам, маем ![]() , г.зн.
, г.зн. ![]() – (бмп). ■
– (бмп). ■
Разгледзім асноўныя ўласцівасці бясконца малых паслядоўнасцяў.
1º. Сума і розніца дзвюх (бмп) ёсць таксама (бмп).
□ Няхай ![]() і
і ![]() – (бмп) г.зн.
– (бмп) г.зн. ![]()
![]()
![]() Назавем
Назавем ![]() . Тады
. Тады ![]() . Паводле М-Лемы
. Паводле М-Лемы ![]() – (бмп). ■
– (бмп). ■
Вынік. Алгебраічная сума канечнай колькасці бясконца малых паслядоўнасцяў ёсць бясконца малая паслядоўнасць.
2º. Здабытак дзвюх (бмп) ёсць таксама (бмп).
□ Няхай ![]() ёсць (бмп),
таму
ёсць (бмп),
таму ![]()
![]()
![]() . Калі ж
. Калі ж ![]() таксама (бмп),
то возьмем
таксама (бмп),
то возьмем ![]() і для яго знойдзем
і для яго знойдзем ![]()
![]() . Няхай
. Няхай ![]() . Тады
. Тады ![]() , г.зн.
, г.зн. ![]() –(бмп). ■
–(бмп). ■
Вынік. Здабытак канечнай колькасці бясконца малых паслядоўнасцяў ёсць бясконца малая паслядоўнасць.
Заўвага. Дзель дзвюх (бмп) можа і не быць (бмп).
Напрыклад, калі ![]() , то
, то ![]() – не ёсць (бмп);
калі ж
– не ёсць (бмп);
калі ж ![]() , то
, то ![]() – (бмп), а
– (бмп), а ![]() – бясконца вялікая
паслядоўнасць,.
– бясконца вялікая
паслядоўнасць,.
3º. Здабытак абмежаванай лікавай паслядоўнасці на (бмп) ёсць (бмп).
□ Няхай ![]() –
абмежаваная лікавая паслядоўнасць, г.зн.
–
абмежаваная лікавая паслядоўнасць, г.зн. ![]()
![]() .
Паколькі ж
.
Паколькі ж ![]() – (бмп), то
– (бмп), то ![]()
![]()
![]() . Такім чынам, маем
. Такім чынам, маем ![]() . Паводле М-Лемы
. Паводле М-Лемы ![]() – (бмп) ■
– (бмп) ■
Вынік. Здабытак бясконца малой паслядоўнасці на
лік ёсць бясконца малая паслядоўнасць, г.зн. ![]() –
(бмп)
–
(бмп) ![]() , калі
, калі ![]() – (бмп).
– (бмп).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.