Няхай на прамавугольніку ![]() вызначана функцыя
вызначана функцыя ![]() . Калі
. Калі ![]() функцыя
функцыя ![]() ёсць інтэгравальная па
ёсць інтэгравальная па ![]() на
на ![]() , то інтэграл
, то інтэграл 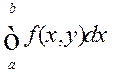 ёсць функцыя ад параметра
ёсць функцыя ад параметра ![]() , вызначаная на
, вызначаная на ![]() . Пры гэтым
. Пры гэтым
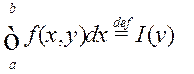 (1)
(1)
называюць інтэгралам, залежным ад параметраy (ІЗАП).
Калі функцыя ![]() вызначана на
мностве больш агульнага выгляду
вызначана на
мностве больш агульнага выгляду
![]()
і на ![]() існуе інтэграл
існуе інтэграл
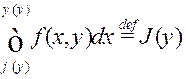 ,
(2)
,
(2)
то гэты інтэграл называюць ІЗАП са зменнымі межамі.
Нагадаем, што функцыя ![]() зменных
зменных
![]() называецца раўнамерна непарыўнаю
на
называецца раўнамерна непарыўнаю
на ![]() , калі
, калі ![]() .
.
□ Паколькі функцыя ![]() ёсць непарыўная на замкнёным абмежаваным
мностве
ёсць непарыўная на замкнёным абмежаваным
мностве ![]() , то паводле тэарэмы Кантара яна
раўнамерна непарыўная на
, то паводле тэарэмы Кантара яна
раўнамерна непарыўная на ![]() , г. зн.
, г. зн.
![]() .
.
Калі ўзяць ![]() , то маем
, то маем
![]() . (3)
. (3)
Тады
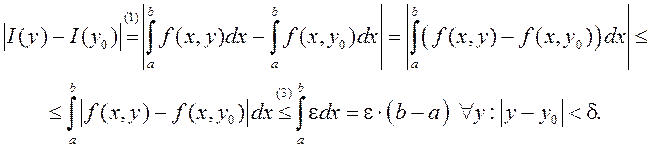
Гэта азначае, што функцыя ![]() –
непарыўная ў кожным пункце
–
непарыўная ў кожным пункце ![]() .■
.■
Заўвага. Можна паказаць, што калі ![]() ёсць непарыўная на
ёсць непарыўная на ![]() і
і ![]() – непарыўныя на
– непарыўныя на ![]() , то
, то ![]() ёсць непарыўная функцыя на
ёсць непарыўная функцыя на ![]() .
.
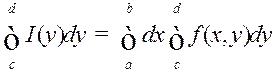 . (4)
. (4)
□ Паколькі ![]() як непарыўная
функцыя (Тэарэма 1) ёсць інтэгравальная. то
як непарыўная
функцыя (Тэарэма 1) ёсць інтэгравальная. то 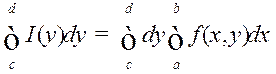 . Апошні інтэграл і інтэграл з правай часткі
роўнасці (4) можна разглядаць як паўторныя для падвойнага інтэграла
. Апошні інтэграл і інтэграл з правай часткі
роўнасці (4) можна разглядаць як паўторныя для падвойнага інтэграла 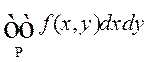 , які існуе для непарыўнай на
, які існуе для непарыўнай на ![]() функцыі. Таму інтэгралы з (4)
супадаюць. ■
функцыі. Таму інтэгралы з (4)
супадаюць. ■
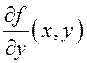 ёсць
непарыўныя на
ёсць
непарыўныя на 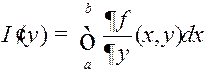 , (5)
, (5)г. зн. 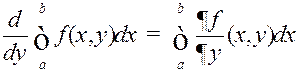 (ІЗАП можна дыферэнцаваць пад знакам інтэграла).
(ІЗАП можна дыферэнцаваць пад знакам інтэграла).
□ Увядзем дапаможную функцыю
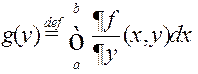 . (6)
. (6)
Паколькі 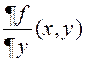 ёсць непарыўная на
ёсць непарыўная на ![]() ,
то згодна з тэарэмаю 1 функцыя
,
то згодна з тэарэмаю 1 функцыя ![]() ёсць
непарыўная на
ёсць
непарыўная на ![]() і інтэграл ад яе можна
вылічыць паводле формулы (4) інтэгравання ІЗАП пад знакам інтэграла:
і інтэграл ад яе можна
вылічыць паводле формулы (4) інтэгравання ІЗАП пад знакам інтэграла:
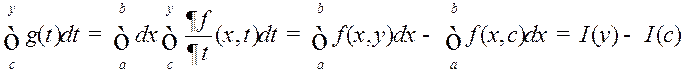 , г. зн.
, г. зн. 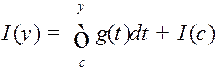 , адкуль на падставе тэарэмы Барроў
, адкуль на падставе тэарэмы Барроў ![]() . Замяняючы ў (6)
. Замяняючы ў (6) ![]() на
на ![]() ,
атрымаем (5). ■
,
атрымаем (5). ■
Формулу (5) называюць правілам Ляйбніца дыферэнцавання ІЗАП.
Заўвага. Калі функцыі ![]() і
і ![]() ёсць непарыўныя на
ёсць непарыўныя на ![]() і
і ![]() –
непарыўна дыферэнцавальныя на
–
непарыўна дыферэнцавальныя на ![]() , то
, то ![]() ёсць непарыўна
дыферэнцавальная функцыя на
ёсць непарыўна
дыферэнцавальная функцыя на ![]() , прычым
, прычым
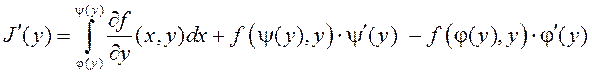 (7)
(7)
– правіла Ляйбніца дыферэнцавання ІЗАП са зменнымі межамі.
Сапраўды, няхай 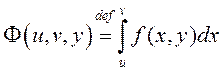 . Тады
. Тады
![]() .
(8)
.
(8)
Функцыя ![]() мае непарыўныя частковыя
вытворныя па ўсім зменным:
мае непарыўныя частковыя
вытворныя па ўсім зменным:
![]() –
згодна з тэарэмаю Барроў;
–
згодна з тэарэмаю Барроў; 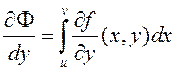 – згодна з
тэарэмаю 3. Тады з (8) на падставе тэарэмы пра вытворную складанай функцыі
– згодна з
тэарэмаю 3. Тады з (8) на падставе тэарэмы пра вытворную складанай функцыі
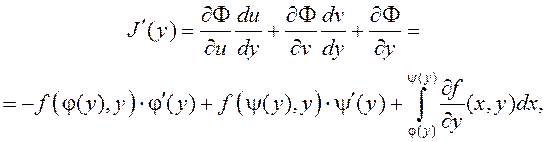
што і азначае праўдзівасць формулы (7).
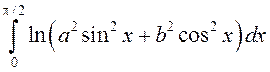 .
. ► Будзем разглядаць гэты
інтэграл як ІЗАП з параметрам ![]() і абазначым
яго праз
і абазначым
яго праз ![]() =.
=.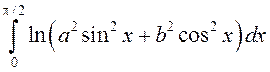 . Тады
. Тады
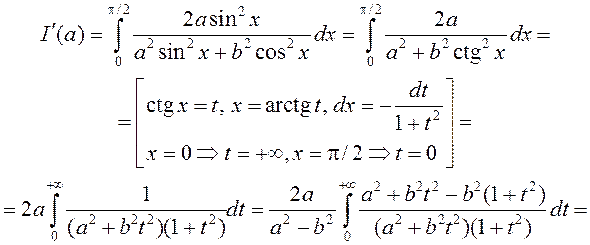
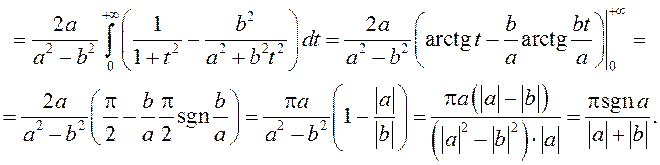
Такім чынам, з роўнасці 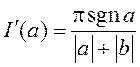 маем
маем
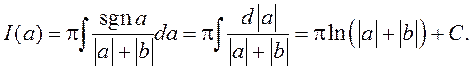
Паколькі з умовы ![]()
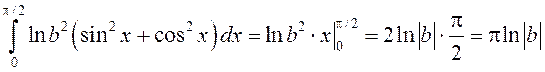 вынікае, што
вынікае, што ![]() ,
то
,
то 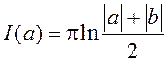 .◄
.◄
Няхай на паласе ![]() вызначана функцыя
вызначана функцыя ![]() . Калі
. Калі ![]() неўласцівы інтэграл
неўласцівы інтэграл 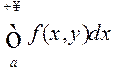 ёсць збежны, то кажуць, што
ён збежны на адрэзку
ёсць збежны, то кажуць, што
ён збежны на адрэзку ![]() . Пры
гэтым на адрэзку
. Пры
гэтым на адрэзку ![]() вызначана функцыя
вызначана функцыя
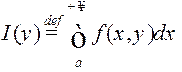 ,
(1)
,
(1)
якую называюць неўласцівым
інтэгралам, залежным ад параметра ![]() (НІЗАП).
(НІЗАП).
Збежнасць НІЗАП 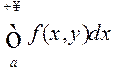 да
функцыі
да
функцыі ![]() азначае існаванне ліміту
азначае існаванне ліміту
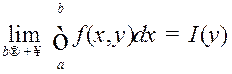 , г. зн.
, г. зн. ![]()
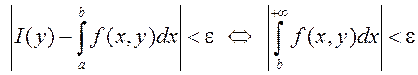 .
.
Такім чынам, НІЗАП (1) ёсць
збежны на адрэзку ![]() , калі і толькі калі
, калі і толькі калі
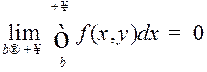 .
.
def. Кажуць, што НІЗАП (1)
збягаецца раўнамерна па параметру у на адрэзку ![]() , калі
, калі ![]()
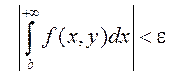 .
.
Калі НІЗАП (1) збягаецца на
адрэзку ![]() , але не ёсць раўнамерна
збежны па параметру
, але не ёсць раўнамерна
збежны па параметру ![]() на
на ![]() , то кажуць,
што НІЗАП (1) збягаецца нераўнамерна па параметру
, то кажуць,
што НІЗАП (1) збягаецца нераўнамерна па параметру ![]() на адрэзку
на адрэзку ![]() г. зн.
г. зн.
![]()
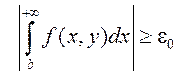 .
.
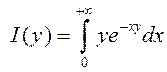 на
адрэзках: 1)
на
адрэзках: 1) ► 1) 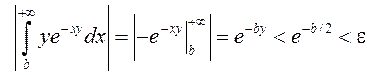
![]() –інтэграл збягаецца раўнамерна.
–інтэграл збягаецца раўнамерна.
2) Паколькі 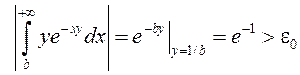 , калі
, калі ![]() . Такім чынам,
. Такім чынам, ![]()
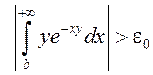 ,
г. зн. інтэграл збягаецца нераўнамерна на
,
г. зн. інтэграл збягаецца нераўнамерна на ![]() .◄
.◄
Заўвага. НІЗАП ![]() – непарыўная на абодвух адрэзках
функцыя , але на першым з іх ён збягаецца раўнамерна, а на другім нераўнамерна,
г. зн. няма аналогіі з тэарэмай Кантара пра раўнамерную непарыўнасць
функцыі .
– непарыўная на абодвух адрэзках
функцыя , але на першым з іх ён збягаецца раўнамерна, а на другім нераўнамерна,
г. зн. няма аналогіі з тэарэмай Кантара пра раўнамерную непарыўнасць
функцыі .
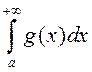 (3)
(3)□ З (2) і з прыкметы параўнання для НІ-1 вынікае, што
НІЗАП (1) ёсць абсалютна збежны на ![]() . Збежнасць інтэграла (3)
азначае:
. Збежнасць інтэграла (3)
азначае:
![]()
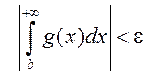 .
.
На падставе няроўнасці (2) маем 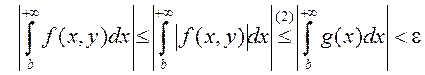 .
.
Такім чынам, атрымалі, што
![]()
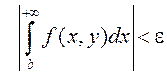 .
.
Гэта і азначае, што НІЗАП (1) ёсць раўнамерна
збежны на ![]() .■
.■
□ Возьмем адвольнае значэнне ![]() . Тады
. Тады
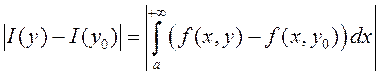 =
=
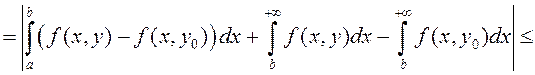
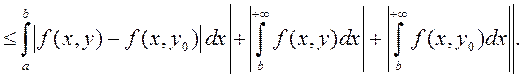
Такім чынам,
![]()
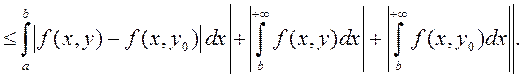 (4)
(4)
Паколькі НІЗАП (1) ёсць раўнамерна збежны, то
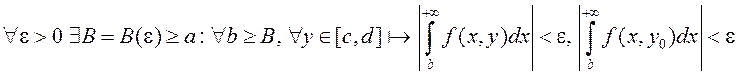 . (5)
. (5)
Зафіксуем пэўнае значэнне ![]() і
разгледзім прамавугольнік
і
разгледзім прамавугольнік ![]() . Паколькі
. Паколькі ![]() ёсць раўнамерна непарыўная на
ёсць раўнамерна непарыўная на ![]() (на падставе тэарэмы Кантара),
то для выбранага раней
(на падставе тэарэмы Кантара),
то для выбранага раней ![]()
![]() .
(6)
.
(6)
З няроўнасцяў (4), (5) і (6) вынікае:
![]()
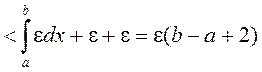 , калі
, калі ![]() , г. зн. функцыя
, г. зн. функцыя ![]() ёсць
непарыўная ў пункце
ёсць
непарыўная ў пункце ![]() , а тым самым на
, а тым самым на ![]() . ■
. ■
Заўвага. Раўнамерная збежнасць не
з’яўляецца неабходнаю ўмоваю для непарыўнасці НІЗАП. У прыкладзе 1 функцыя ![]() – непарыўная на
– непарыўная на ![]() , хаця НІЗАП
, хаця НІЗАП ![]() не з’яўляецца раўнамерна збежным
на гэтым адрэзку.
не з’яўляецца раўнамерна збежным
на гэтым адрэзку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.