БЕЛАРУСКІ ДЗЯРЖАЎНЫ УНІВЕРСІТЭТ
ФІЗІЧНЫ ФАКУЛЬТЭТ
КАФЕДРА ВЫШЭЙШАЙ МАТЭМАТЫКІ І МАТЭМАТЫЧНАЙ ФІЗІКІ
ВЫШЭЙШАЯ МАТЭМАТЫКА
У ПРЫКЛАДАХ І ЗАДАЧАХ
Вучэбны дапаможнік для студэнтаў
фізічнага і радыёфізічнага факультэтаў
У пяці частках
Частка 1. Матэматычны аналіз 1
МІНСК
2006
УДК
ББК
Рэкамендавана Вучоным саветам
фізічнага факультэта
Аўтары - складальнікі:
, , , , Α.
Рэцэнзенты:
член-карэспандэнтАкадэміі навук Рэспублікі Беларусь,
прафесар ;
кандыдат фізіка–матэматычных навук,
дацэнт
Вышэйшая матэматыка ў прыкладах і задачах. Вучэбны дапаможнік для студэнтаў фізічнага і радыёфізічнага факультэтаў. У 5 ч. Ч.1 / Аўт.- склад. : і інш. – Мн.: БДУ, 2006. – с.
Дапаможнік складаецца з пяці частак і прызначаецца для студэнтаў фізічнага і радыёфізічнага факультэтаў. Матэрыял адпавядае праграме вышэйшай матэматыкі. У кожным параграфе падаецца значная колькасць прыкладаў і задач, перад якімі змешчаны кароткія тэарэтычныя звесткі і разгледжаны тыповыя прыклады. Першая частка дапаможніка змяшчае матэрыял з матэматычнага аналізу функцый адной зменнай.
Дапаможнік дапасаваны да падручніка “Курс вышэйшай матэматыкі” (аўтары В. Русак, Л. Шлома, В. , Α. Крачкоўскі. Мн.: Выш. шк., 1994)
УДК
ББК
© БДУ, 2006
1º. Мноства –
першаснае (неазначальнае) паняцце. Абазначаюць мноствы вялікімі лацінскімі
літарамі A, B, C, X,...; ![]() – мноства натуральных
лікаў,
– мноства натуральных
лікаў, ![]() – цэлых,
– цэлых, ![]() – рацыянальных,
– рацыянальных, ![]() – рэчаісных. Тое, што элемент x належыць мноству A, абазначаюць x
– рэчаісных. Тое, што элемент x належыць мноству A, абазначаюць x![]() A; калі x не
з’яўляецца элементам A – x
A; калі x не
з’яўляецца элементам A – x![]() А. Ужываюць запіс:
А. Ужываюць запіс: ![]() ,
які паказвае, што
,
які паказвае, што ![]() з’яўляюцца элементамі
мноства X (і толькі яны); а
таксама X={x: M(x)},які
характарызуе мноства X як
сукупнасць элементаў x, што
задавальняюць умову M(x).
з’яўляюцца элементамі
мноства X (і толькі яны); а
таксама X={x: M(x)},які
характарызуе мноства X як
сукупнасць элементаў x, што
задавальняюць умову M(x).
Калі кожны элемент мноства А ёсць
элемент мноства В, то кажуць:
" А ёсць падмноства мноства В " ці "
А улучана ў В " і пішуць А![]() В
(або В
В
(або В![]() А). Два мноствы А і
В называюцца роўнымі (абазначаюць
А). Два мноствы А і
В называюцца роўнымі (абазначаюць ![]() ),
калі яны складаюцца з адных і тых самых элементаў:
),
калі яны складаюцца з адных і тых самых элементаў: ![]() ,
калі і толькі калі
,
калі і толькі калі ![]()
![]() і
і ![]() .
Мноства, якое не мае элементаў, называецца пустым і абазначаецца
.
Мноства, якое не мае элементаў, называецца пустым і абазначаецца ![]() .
.
Аперацыі з мноствамі азначаюцца наступным чынам:
1) перасячэнне мностваў ![]() ;
;
2) аб’яднанне мностваў ![]() ;
;
3) розніца мностваў ![]() ;
;
4) дапаўненне мноства А
(да пэўнага універсальнага мноства ![]() )
)
![]() .
.
Для адвольных мностваў А, В, С справядлівы ўласцівасці:
1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ;
6)
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ;10)
;10) ![]() .
.
Колькасць элементаў канечнага мноства А абазначаецца праз m(A). Тады для адвольных канечных мностваў А, В праўдзіцца роўнасць:
![]() . (1.1)
. (1.1)
2º. Сума
зададзеных ![]() лікаў
лікаў ![]() запісваецца
запісваецца ![]() . Літара
. Літара ![]() называецца індэксам
сумавання. Сума не залежыць ад таго, якой літарай пазначаны індэкс
сумавання, г. зн.
называецца індэксам
сумавання. Сума не залежыць ад таго, якой літарай пазначаны індэкс
сумавання, г. зн. 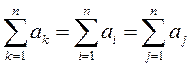 . Часам узнікае
неабходнасць зрушыць межы змянення індэкса сумавання ў той або іншы бок.
Напрыклад,
. Часам узнікае
неабходнасць зрушыць межы змянення індэкса сумавання ў той або іншы бок.
Напрыклад, 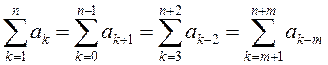 . Аперацыя сумавання мае
ўласцівасць лінейнасці
. Аперацыя сумавання мае
ўласцівасць лінейнасці 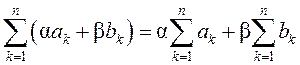 . Суму
. Суму ![]() складнікаў
складнікаў ![]() запісваюць у выглядзе
запісваюць у выглядзе 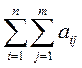 і называюць падвойнаю
сумай. Пры гэтым мае месца роўнасць
і называюць падвойнаю
сумай. Пры гэтым мае месца роўнасць
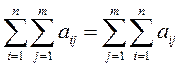 .
.
3º. Для
доказу праўдзівасці сцверджання ![]() часта
звяртаюцца да метаду матэматычнай індукцыі – сцверджанне
часта
звяртаюцца да метаду матэматычнай індукцыі – сцверджанне ![]() лічаць праўдзівым для ўсіх
лічаць праўдзівым для ўсіх ![]() , калі выконваюцца наступныя
дзве ўмовы:
1) выказванне
, калі выконваюцца наступныя
дзве ўмовы:
1) выказванне ![]() праўдзівае пры
праўдзівае пры ![]() ; 2) з праўдзівасці
выказвання
; 2) з праўдзівасці
выказвання ![]() вынікае праўдзівасць выказвання
вынікае праўдзівасць выказвання
![]() для ўсіх натуральных k. Умова праўдзівасці выказвання
для ўсіх натуральных k. Умова праўдзівасці выказвання ![]() , называецца базай
індукцыі, а меркаванне праўдзівасці выказвання
, называецца базай
індукцыі, а меркаванне праўдзівасці выказвання ![]() – індуктыўным пагадненнем.
Калі задачай абумоўлена, што выказванне
– індуктыўным пагадненнем.
Калі задачай абумоўлена, што выказванне ![]() разглядаецца
пачынаючы з пэўнага ліку
разглядаецца
пачынаючы з пэўнага ліку ![]() (не з ліку
1), то базай індукцыі з’яўляецца праўдзівасць выказвання
(не з ліку
1), то базай індукцыі з’яўляецца праўдзівасць выказвання ![]() , а індуктыўнае пагадненне
тычыцца адвольнага натуральнага k,
, а індуктыўнае пагадненне
тычыцца адвольнага натуральнага k, ![]() .
.
►Мноства ўсіх студэнтаў
першага курса факультэта будзем лічыць універсальным і абазначым U; M – мноства студэнтаў, якія здалі залік па матэматыцы, F – па фізіцы. Нам трэба знайсці колькасць m(M∩F). Мноства
студэнтаў, якія не здалі ніводнаго заліку, ёсць ![]() прычым
згодна з умовай задачы m(
прычым
згодна з умовай задачы m(![]() . Паколькі для дапаўнення
мностваў справядліва ўласцівасць
. Паколькі для дапаўнення
мностваў справядліва ўласцівасць ![]() , то і m(
, то і m(![]() .
Тады
.
Тады ![]() .
.
На падставе формулы (1.1) атрымліваем
![]() ◄
◄
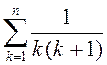 .
.► Задачу пра вылічэнне
сумы 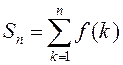 , дзе
, дзе ![]() – зададзеная функ-цыя, звычайна
разглядаюць як задачу знаходжання
– зададзеная функ-цыя, звычайна
разглядаюць як задачу знаходжання ![]() як функцыі
ад
як функцыі
ад ![]() . Напрыклад, калі
. Напрыклад, калі ![]() , то
, то
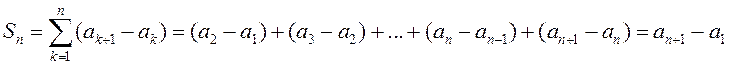 .
.
Паколькі 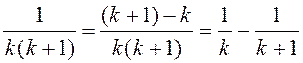 ,
то
,
то
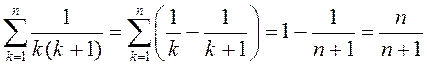 . ◄
. ◄
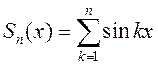 .
. Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.